2015-2016学年浙江省台州市临海市七年级上学期期末数学试卷
试卷更新日期:2017-01-03 类型:期末考试
一、选择题
-
1. ﹣2的绝对值是( )A、﹣2 B、﹣ C、2 D、2. 单项式﹣xy2的系数是( )A、1 B、﹣1 C、2 D、33. 如图,这是由大小相同的长方体木块搭成的立体图形,则从正面看这个立体图形,得到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )
4. 将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )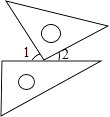 A、30°10′ B、60°10′ C、59°50′ D、60°50′5. 下列运算正确的是( )A、5x2y﹣4x2y=x2y B、x﹣y=xy C、x2+3x3=4x5 D、5x3﹣2x3=26. 若关于x的方程ax=3x﹣2的解是x=1,则a的值是( )A、﹣1 B、﹣5 C、5 D、17.
A、30°10′ B、60°10′ C、59°50′ D、60°50′5. 下列运算正确的是( )A、5x2y﹣4x2y=x2y B、x﹣y=xy C、x2+3x3=4x5 D、5x3﹣2x3=26. 若关于x的方程ax=3x﹣2的解是x=1,则a的值是( )A、﹣1 B、﹣5 C、5 D、17.如图,某轮船在O处,测得灯塔A在它北偏东40°的方向上,渔船B在它的东南方向上,则∠AOB的度数是( )
 A、85° B、90° C、95° D、100°8. 若有理数m在数轴上对应的点为M,且满足m<1<﹣m,则下列数轴表示正确的是( )A、
A、85° B、90° C、95° D、100°8. 若有理数m在数轴上对应的点为M,且满足m<1<﹣m,则下列数轴表示正确的是( )A、 B、
B、 C、
C、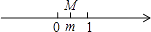 D、
D、 9. 用[x]表示不大于x的整数中最大的整数,如[2.4]=2,[﹣3.1]=﹣4,请计算[5.5]+[﹣4 ]=( )A、﹣1 B、0 C、1 D、210.
9. 用[x]表示不大于x的整数中最大的整数,如[2.4]=2,[﹣3.1]=﹣4,请计算[5.5]+[﹣4 ]=( )A、﹣1 B、0 C、1 D、210.点O在直线AB上,点A1 , A2 , A3 , …在射线OA上,点B1 , B2 , B3 , …在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,以每秒1个单位长度的速度按如图所示的箭头方向沿着实线段和以点O为圆心的半圆匀速运动,即从OA1B1B2→A2…按此规律,则动点M到达A10点处所需时间为( )秒.
 A、10+55π B、20+55π C、10+110π D、20+110π
A、10+55π B、20+55π C、10+110π D、20+110π二、填空题
-
11. 写出一个在﹣1 和1 之间的整数 .12. 单项式﹣3xny2是5次单项式,则n= .13. 2015年,天猫双十一全球狂欢节销售实际成交值超过912亿,将91200000000用科学记数法表示为 .14. 如图,CD是线段AB上两点,若CB=4cm,DB=7cm,且D是AC中点,则AC的长等于
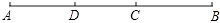 15. 要把一根木条在墙上钉牢,至少需要枚钉子.其中的道理是16. 如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=°.
15. 要把一根木条在墙上钉牢,至少需要枚钉子.其中的道理是16. 如图,∠1=20°,∠AOC=90°,点B,O,D在同一直线上,则∠2=°. 17. 若多项式x2+2x的值为5,则多项式2x2+4x+7的值为 .18. 有一个数值转换器,其工作原理如图所示,若输入的数据是3,则输出的结果是 .
17. 若多项式x2+2x的值为5,则多项式2x2+4x+7的值为 .18. 有一个数值转换器,其工作原理如图所示,若输入的数据是3,则输出的结果是 .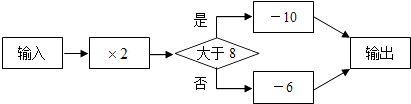 19. 从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲乙两地相距x千米,则列方程为20. 如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且BC=4厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发在直线上运动,则经过秒时线段PQ的长为5厘米.
19. 从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲乙两地相距x千米,则列方程为20. 如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且BC=4厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发在直线上运动,则经过秒时线段PQ的长为5厘米.
三、解答题
-
21. 计算:(1)、﹣10+5﹣3(2)、﹣22÷(﹣4)﹣6×( + ).22. 先化简,再求值:4a2+2a﹣2(2a2﹣3a+4),其中a=2.23. 解方程:(1)、5x﹣3=4x+15(2)、 .
24.作图:(温馨提醒:确认后,在答题纸上用黑色水笔描黑)
如图,已知平面上有四个点A,B,C,D

(1)作射线AD;
(2)作直线BC与射线AD交于点E;
(3)连接AC,再在AC的延长线上作线段CP=AC.
(要求尺规作图,保留作图痕迹,不写作图步骤)
25. 春节将至,某移动公司计划推出两种新的计费方式,如下表所示:方式1
方式2
月租费
30元/月
0
本地通话费
0.20元/分钟
0.40元/分钟
请解决以下两个问题:(通话时间为正整数)
(1)、若本地通话100分钟,按方式一需交费多少元?按方式二需交费多少元?(2)、对于某月本地通话,当通话多长时间时,按两种计费方式的收费一样多?26. 把几个数用大括号括起来,相邻两个数之间用逗号隔开,如:{1,2},{1,4,7},…,我们称之为集合,其中的每一个数称为该集合的元素,如果一个所有元素均为有理数的集合满足:当有理数x是集合的一个元素时,2016﹣x也必是这个集合的元素,这样的集合我们又称为黄金集合.例如{0,2016}就是一个黄金集合,(1)、集合{2016}黄金集合,集合{﹣1,2017}黄金集合;(两空均填“是”或“不是”)(2)、若一个黄金集合中最大的一个元素为4016,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;(3)、若一个黄金集合所有元素之和为整数M,且24190<M<24200,则该集合共有几个元素?说明你的理由.27. 将一副直角三角板如图1摆放在直线AD上(直角三角板OBC和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC不动,将三角板MON绕点O以每秒10°的速度顺时针旋转,旋转时间为t秒 (1)、当t=秒时,OM平分∠AOC?如图2,此时∠NOC﹣∠AOM=°;
(1)、当t=秒时,OM平分∠AOC?如图2,此时∠NOC﹣∠AOM=°; (2)、继续旋转三角板MON,如图3,使得OM、ON同时在直线OC的右侧,猜想∠NOC与∠AOM有怎样的数量关系?并说明理由;
(2)、继续旋转三角板MON,如图3,使得OM、ON同时在直线OC的右侧,猜想∠NOC与∠AOM有怎样的数量关系?并说明理由; (3)、若在三角板MON开始旋转的同时,另一个三角板OBC也绕点O以每秒5°的速度顺时针旋转,当OM旋转至射线OD上时同时停止,(自行画图分析)
(3)、若在三角板MON开始旋转的同时,另一个三角板OBC也绕点O以每秒5°的速度顺时针旋转,当OM旋转至射线OD上时同时停止,(自行画图分析)①当t=秒时,OM平分∠AOC?
(4)、②请直接写出在旋转过程中,∠NOC与∠AOM的数量关系.