2015-2016学年浙江省台州市临海市九年级上学期期末数学试卷

试卷更新日期：2017-01-03 类型：期末考试

进入出卷网下载

一、选择题

1. 下列函数的图象是双曲线的是（　　）

A、y=2x﹣1 B、y= $\frac{1}{x}$ C、y=x D、y=x²

查看试题解析
2. 下列事件是随机事件的是（）

A、火车开到月球上 B、抛出的石子会下落 C、明天临海会下雨 D、早晨的太阳从东方升起

查看试题解析
3. 二次函数y=x²+4x﹣5的图象的对称轴为（）

A、x=4 B、x=﹣4 C、x=2 D、x=﹣2

查看试题解析
4. 如图，⊙O是△ABC的内切圆，D，E是切点，∠A=50°，∠C=60°，则∠DOE=（）

A、70° B、110° C、120° D、130°

查看试题解析
5. 如图，把△ABC绕着点A顺时针方向旋转34°，得到△AB′C′，点C刚好落在边B′C′上．则∠C′=（）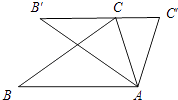

A、56° B、62° C、68° D、73°

查看试题解析
6. 将抛物线y=3x²先向左平移一个单位，再向上平移一个单位，两次平移后得到的抛物线解析式为（）

A、y=3（x+1）²+1 B、y=3（x+1）²﹣1 C、y=3（x﹣1）²+1 D、y=3（x﹣1）²﹣1

查看试题解析
7. 小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸板的面积是（）

A、120πcm² B、240πcm² C、260πcm² D、480πcm²

查看试题解析
8. 用锤子以均匀的力敲击铁钉入木板．随着铁钉的深入，铁钉所受的阻力会越来越大，使得每次钉入木板的钉子的长度后一次为前一次的k倍（0＜k＜1）．已知一个钉子受击3次后恰好全部进入木板，且第一次受击后进入木板部分的铁钉长度是钉长的 $\frac{4}{7}$ ．设铁钉的长度为1，那么符合这一事实的方程是（）

A、 $\frac{4}{7}$ （1+k）²=1 B、 $\frac{4}{7}$ k+ $\frac{4}{7}$ k²=1 C、 $\frac{4}{7}$ + $\frac{4}{7}$ k+ $\frac{4}{7}$ k²=1 D、 $\frac{4}{7}$ + $\frac{4}{7}$ （1+k）²=1

查看试题解析
9. 利用平方根去根号可以构造一个整系数方程．例如：x= $\sqrt{2}$ +1时，移项得x﹣1= $\sqrt{2}$ ，两边平方得（x﹣1）²=（ $\sqrt{2}$ ）² ，所以x²﹣2x+1=2，即x²﹣2x﹣1=0．仿照上述构造方法，当x= $\frac{\sqrt{6} - 1}{2}$ 时，可以构造出一个整系数方程是（）

A、4x²+4x+5=0 B、4x²+4x﹣5=0 C、x²+x+1=0 D、x²+x﹣1=0

查看试题解析
10. 如图，在y轴正半轴上依次截取OA₁=A₁A₂=A₂A₃=…=A_n_﹣₁A_n（n为正整数），过A₁ ， A₂ ， A₃ ， …，A_n分别作x轴的平行线，与反比例函数y= $\frac{2}{x}$ （x＞0）交于点B₁ ， B₂ ， B₃ ， …，B_n ，如图所示的Rt△B₁C₁B₂ ， Rt△B₂C₂B₃ ， Rt△B₃C₃B₄ ， …，Rt△B_n_﹣₁C_n_﹣₁B_n面积分别记为S₁ ， S₂ ， S₃ ， …，S_n_﹣₁ ，则S₁+S₂+S₃+…+S_n_﹣₁=（）

A、1 B、2 C、1﹣ $\frac{1}{n}$ D、2﹣ $\frac{1}{n}$

查看试题解析

二、填空题

11. 点A（1，19）与点B关于原点中心对称，则点B的坐标为

查看试题解析
12. 如果反比例函数 $y = \frac{m - 3}{x}$ 的图象在x＜0的范围内，y随x的增大而减小，那么m的取值范围是．

查看试题解析
13. 如图，点O是正五边形ABCDE的中心，则∠BAO的度数为．

查看试题解析
14. 一个盒子中装有大小、形状一模一样的白色弹珠和黑色弹珠，从盒中随机取出一颗弹珠，取得白色弹珠的概率是 $\frac{1}{3}$ ．如果盒子中白色弹珠有4颗，则盒中有黑色弹珠颗．

查看试题解析
15. 如图，正方形ABCD的顶点A，B与正方形EFGH的顶点G，H同在一段抛物线上，且抛物线的顶点同时落在CD和y轴上，正方形边AB与EF同时落在x轴上，若正方形ABCD的边长为4，则正方形EFGH的边长为

查看试题解析
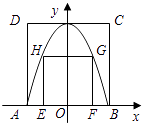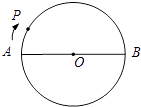
16.
如图，在⊙O中，AB为⊙O的直径，AB=4．动点P从A点出发，以每秒π个单位的速度在⊙O上按顺时针方向运动一周．设动点P的运动时间为t秒，点C是圆周上一点，且∠AOC=40°，当t=秒时，点P与点C中心对称，且对称中心在直径AB上．

查看试题解析

三、解答题

17. 解方程：

(1)、4x²﹣20=0；

(2)、x²+3x﹣1=0．

查看试题解析
18. 动手画一画，请把下图补成以A为对称中心的中心对称图形．

查看试题解析
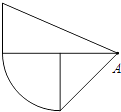19. 如图，AB是⊙O的直径，点C是⊙O上一点，连接BC，AC，OD⊥BC于E．

(1)、求证：OD∥AC；

(2)、若BC=8，DE=3，求⊙O的直径．

查看试题解析
20. 已知关于x的一元二次方程x²+2（k﹣1）x+k²﹣1=0有两个不相等的实数根．

(1)、求实数k的取值范围；

(2)、0可能是方程的一个根吗？若是，请求出它的另一个根；若不是，请说明理由．

查看试题解析
21. 一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，4，5，x．甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复试验．实验数据如下表：
摸球总次数
10
20
30
60
90
120
180
240
330
450
“和为8”出现的频数
2
10
13
24
30
37
58
82
110
150
“和为8”出现的频率
0.20
0.50
0.43
0.40
0.33
0.31
0.32
0.34
0.33
0.33
解答下列问题：

(1)、如果实验继续进行下去，根据上表数据，出现“和为8”的频率将稳定在它的概率附近．估计出现“和为8”的概率是；

(2)、当x=7时，请用列表法或树状图法计算“和为8”的概率；并判断x=7是否可能．

查看试题解析
22. 如图是一种新型娱乐设施的示意图，x轴所在位置记为地面，平台AB∥x轴，OA=6米，AB=2米，BC是反比例函数y= $\frac{k}{x}$ 的图象的一部分，CD是二次函数y=﹣x²+mx+n图象的一部分，连接点C为抛物线的顶点，且C点到地面的距离为2米，D点是娱乐设施与地面的一个接触点．

(1)、试求k，m，n的值；

(2)、试求点B与点D的水平距离．

查看试题解析
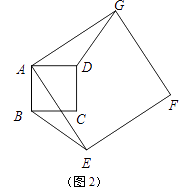
23.
如图1，正方形ABCD与正方形AEFG的边AB，AE（AB＜AE）在一条直线上，正方形AEFG以点A为旋转中心逆时针旋转，设旋转角为α．在旋转过程中，两个正方形只有点A重合，其它顶点均不重合，连接BE，DG．

(1)、
当正方形AEFG旋转至如图2所示的位置时，求证：BE=DG；

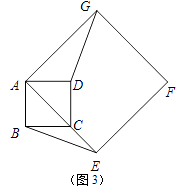
(2)、
如图3，如果α=45°，AB=2，AE=3 $\sqrt{3}$ ．
①求BE的长；②求点A到BE的距离；

(3)、当点C落在直线BE上时，连接FC，直接写出∠FCD的度数．

查看试题解析
24. 定义：把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”．
如图，抛物线y=x²﹣2x﹣3与x轴交于点A，B，与y轴交于点D，以AB为直径，在x轴上方作半圆交y轴于点C，半圆的圆心记为M，此时这个半圆与这条抛物线x轴下方部分组成的图形就称为“蛋圆”．

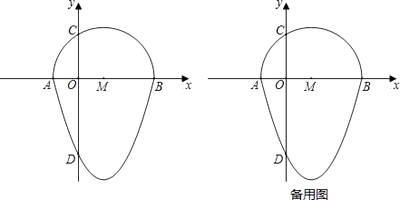(1)、直接写出点A，B，C的坐标及“蛋圆”弦CD的长；
A ， B ， C ， CD=；

(2)、如果一条直线与“蛋圆”只有一个交点，那么这条直线叫做“蛋圆”的切线．
①求经过点C的“蛋圆”切线的解析式；
②求经过点D的“蛋圆”切线的解析式；

(3)、由（2）求得过点D的“蛋圆”切线与x轴交点记为E，点F是“蛋圆”上一动点，试问是否存在S_△_CDE=S_△_CDF ，若存在请求出点F的坐标；若不存在，请说明理由；

(4)、点P是“蛋圆”外一点，且满足∠BPC=60°，当BP最大时，请直接写出点P的坐标．

查看试题解析

摸球总次数	10	20	30	60	90	120	180	240	330	450
“和为8”出现的频数	2	10	13	24	30	37	58	82	110	150
“和为8”出现的频率	0.20	0.50	0.43	0.40	0.33	0.31	0.32	0.34	0.33	0.33