2015-2016学年浙江省台州市临海市八年级上学期期末数学试卷

试卷更新日期：2017-01-03 类型：期末考试

进入出卷网下载

一、精心选一选

1. 下列各式中是分式的是（）

A、x B、 $\frac{x}{2}$ C、 $\frac{2}{x}$ D、 $\frac{1}{3}$

查看试题解析
2. 在下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算结果正确的是（）

A、x•x²=x² B、（x⁵）³=x⁸ C、（ab）³=a³b³ D、a⁶÷a²=a³

查看试题解析
4. 王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（）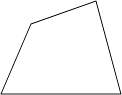

A、0根 B、1根 C、2根 D、3根

查看试题解析
5. 下列等式从左到右的变形是因式分解的是（）

A、6a²b=3a•2ab B、（x+4）（x﹣4）=x²﹣16 C、2ax﹣2ay=2a（x﹣y） D、4x²+8x﹣1=4x（x+2）﹣1

查看试题解析
6. 如图，AE∥FD，AE=FD，要使△EAC≌△FDB，需要添加下列选项中的（）

A、AB=BC B、EC=BF C、∠A=∠D D、AB=CD

查看试题解析
7. 如图，将等腰直角三角形沿虚线裁去顶角后，∠1+∠2=（）

A、225° B、235° C、270° D、300°

查看试题解析
8. 如图，设k= $\frac{甲图中阴影部分面积}{乙图中阴影部分面积}$ （a＞b＞0），则有（）

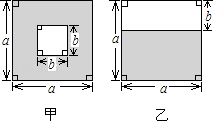A、k＞2 B、1＜k＜2 C、 $\frac{1}{2} < k < 1$ D、 $0 < k < \frac{1}{2}$

查看试题解析
9.
如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（）

A、转化思想 B、三角形的两边之和大于第三边 C、两点之间，线段最短 D、三角形的一个外角大于与它不相邻的任意一个内角

查看试题解析
10. 请你计算：（1﹣x）（1+x），（1﹣x）（1+x+x²），…，猜想（1﹣x）（1+x+x²+…+xⁿ）的结果是（）

A、1﹣xⁿ⁺¹ B、1+xⁿ⁺¹ C、1﹣xⁿ D、1+xⁿ

查看试题解析

二、细心填一填

11. 计算：2x³÷x= ．

查看试题解析
12. 若分式 $\frac{2}{a + 1}$ 有意义，则a的取值范围是．

查看试题解析
13. 因式分解：x﹣x²= ．

查看试题解析
14. 点（2015，﹣2016）关于x轴对称的点的坐标为

查看试题解析
15. 等腰三角形的两边长分别为1和2，其周长为．

查看试题解析
16.
如图是某时刻在镜子中看到准确时钟的情况，则实际时间是

查看试题解析
17. 如图，在Rt△ABC中，∠ACB=90°，∠A=15°，AB的垂直平分线与AC交于点D，与AB交于点E，连接BD．若AD=12cm，则BC的长为 cm．

查看试题解析
18. 已知a+ $\frac{1}{a}$ =3，则a²+ $\frac{1}{a^{2}}$ 的值是．

查看试题解析
19. 如图，若∠B=40°，A、C分别为角两边上的任意一点，连接AC，∠BAC与∠ACB的平分线交于点P₁ ，则∠P₁= ， D、F也为角两边上的任意一点，连接DF，∠BFD与∠FDB的平分线交于点P₂ ， …按这样规律，则∠P₂₀₁₆= ．

查看试题解析
20. 如图，在正方形ABCD中，边AD绕点A顺时针旋转角度m（0°＜m＜360°），得到线段AP，连接PB，PC．当△BPC是等腰三角形时，m的值为

查看试题解析

三、耐心解一解

21. 解答

(1)、计算：2（x+y）（x﹣y）﹣（x+y）²；

(2)、解方程： $\frac{x}{x - 2} + 1 = \frac{4}{x - 2}$ ；

(3)、先化简，再求值：v，在0，1，2三个数中选一个合适的数并代入求值．

查看试题解析
22. 在棋盘中建立如图所示的平面直角坐标系，三颗棋子A，O，B的位置如图所示，它们的坐标分别是（﹣1，1），（0，0）和（1，0）

(1)、如图，添加棋子C，使A，O，B，C四颗棋子成为一个轴对称图形，请在图中画出该图形的对称轴；

(2)、在其他个点位置添加一颗棋子P，使A，O，B，P四颗棋子成为一个轴对称图形，请直接写出棋子P的位置坐标（写出2个即可）．

查看试题解析
23. 列方程或方程组解应用题：
为了培育和践行社会主义核心价值观，引导学生广泛阅读古今文学名著，传承优秀传统文化，我区某校决定为初三学生购进相同数量的名著《三国演义》和《红岩》．其中《三国演义》的单价比《红岩》的单价多28元．若学校购买《三国演义》用了1200元，购买《红岩》用了400元，求《三国演义》和《红岩》的单价各多少元．

查看试题解析
24. 如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．

(1)、求证：△ADC≌△CEB．

(2)、AD=5cm，DE=3cm，求BE的长度．

查看试题解析
25. “综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．

(1)、用记号（a，b，c）（a≤b≤c）表示一个满足条件的三角形，如（2，3，3）表示边长分别为2，3，3个单位长度的一个三角形．请列举出所有满足条件的三角形．

(2)、用直尺和圆规作出三边满足a＜b＜c的三角形（用给定的单位长度，不写作法，保留作图痕迹）．
$\frac{1}{单位长度}$

查看试题解析
26. 在△ABC和△DEC中，AC=BC，DC=EC，∠ACB=∠ECD=90°

(1)、如图1，当点A、C、D在同一条直线上时，AC=12，EC=5
①求证：AF⊥BD ②求AF的长度；

(2)、如图2，当点A、C、D不在同一条直线上时，求证：AF⊥BD；

(3)、如图3，在（2）的条件下，连接CF并延长CF交AD于点G，∠AFG是一个固定的值吗？若是，求出∠AFG的度数；若不是，请说明理由

查看试题解析