2015-2016学年浙江省绍兴市长城教育集团八年级上学期期末数学试卷
试卷更新日期:2017-01-03 类型:期末考试
一、选择题
-
1. 如图所示图案中,轴对称图形是( )A、
 B、
B、 C、
C、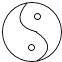 D、
D、 2. 如果a>b,那么下列各式中正确的是( )A、a﹣3<b﹣3 B、 C、﹣a>﹣b D、﹣2a<﹣2b3. 平面直角坐标系中,在第四象限的点是( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)4. 在△ABC中和△DEF中,已知BC=EF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )A、AC=DF B、AB=DE C、∠A=∠D D、∠B=∠E5. 下列命题中,真命题是( )A、周长相等的锐角三角形都全等 B、周长相等的直角三角形都全等 C、周长相等的钝角三角形都全等 D、周长相等的等腰直角三角形都全等6. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:57. 正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A、
2. 如果a>b,那么下列各式中正确的是( )A、a﹣3<b﹣3 B、 C、﹣a>﹣b D、﹣2a<﹣2b3. 平面直角坐标系中,在第四象限的点是( )A、(1,2) B、(1,﹣2) C、(﹣1,2) D、(﹣1,﹣2)4. 在△ABC中和△DEF中,已知BC=EF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )A、AC=DF B、AB=DE C、∠A=∠D D、∠B=∠E5. 下列命题中,真命题是( )A、周长相等的锐角三角形都全等 B、周长相等的直角三角形都全等 C、周长相等的钝角三角形都全等 D、周长相等的等腰直角三角形都全等6. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:57. 正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A、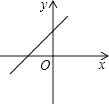 B、
B、 C、
C、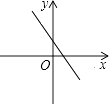 D、
D、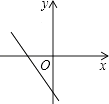 8. 如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
8. 如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( ) A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+39. 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
A、y=2x+3 B、y=x﹣3 C、y=2x﹣3 D、y=﹣x+39. 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )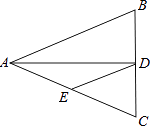 A、20 B、12 C、14 D、1310. 你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x,瓶中水面的高度为Y,下面能大致表示上面故事情节的图象是( )A、
A、20 B、12 C、14 D、1310. 你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x,瓶中水面的高度为Y,下面能大致表示上面故事情节的图象是( )A、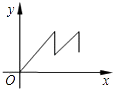 B、
B、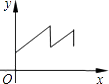 C、
C、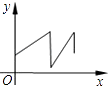 D、
D、
二、填空题
-
11. 把“同位角相等”写成“如果…那么…”的形式为:为 .12. 点A(﹣3,1)关于x轴对称的点的坐标为13. 函数y= 中,自变量x的取值范围是 .14. 如图,函数y=2x和y=ax+4的图象相交于A(m,3),则不等式2x<ax+4的解为 .
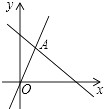 15. 如图,在△ABC中,BC边的垂直平分线交BC于D,交AD于E,若CE平分∠ACB,∠B=40°,则∠A=度.
15. 如图,在△ABC中,BC边的垂直平分线交BC于D,交AD于E,若CE平分∠ACB,∠B=40°,则∠A=度.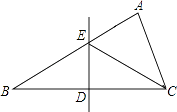 16. 小王与小李约定下午3点在学校门口见面,为此,他们在早上8点将自己的手表对准,小王于下午3点到达学校门口,可是小李还没到,原来小李的手表比正确时间每小时慢4分钟.如果小李按他自己的手表在3点到达,则小王还需要等分钟(正确时间).
16. 小王与小李约定下午3点在学校门口见面,为此,他们在早上8点将自己的手表对准,小王于下午3点到达学校门口,可是小李还没到,原来小李的手表比正确时间每小时慢4分钟.如果小李按他自己的手表在3点到达,则小王还需要等分钟(正确时间).三、解答题
-
17. 解下列不等式组,并将解集在数轴上表示出来.
.
18. 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.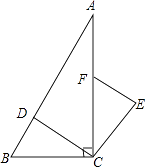 (1)、求证:△BCD≌△FCE;(2)、若EF∥CD,求∠BDC的度数.19. 已知:A(0,1),B(2,0),C(4,3)(1)、在坐标系中描出各点,画出△ABC.
(1)、求证:△BCD≌△FCE;(2)、若EF∥CD,求∠BDC的度数.19. 已知:A(0,1),B(2,0),C(4,3)(1)、在坐标系中描出各点,画出△ABC.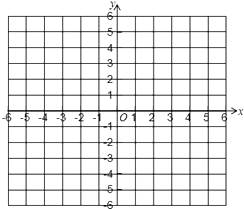 (2)、求△ABC的面积;(3)、设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.20. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.(1)、在图1中以格点为顶点画一个面积为5的正方形;
(2)、求△ABC的面积;(3)、设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.20. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.(1)、在图1中以格点为顶点画一个面积为5的正方形; (2)、在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 、 ;
(2)、在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、 、 ; (3)、如图3,A、B、C是小正方形的顶点,求∠ABC.
(3)、如图3,A、B、C是小正方形的顶点,求∠ABC.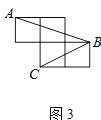 21. 某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
21. 某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)、若工厂计划获利14万元,问A,B两种产品应分别生产多少件?(2)、若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?(3)、在(2)的条件下,哪种生产方案获利最大?并求出最大利润.22. 如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.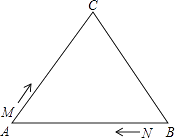 (1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动几秒后,可得到等边三角形△AMN?(3)、当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
(1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动几秒后,可得到等边三角形△AMN?(3)、当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.