2015-2016学年浙江省绍兴市嵊州市八年级上学期期末数学试卷
试卷更新日期:2017-01-03 类型:期末考试
一、选择题
-
1. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数是( )A、75° B、60° C、45° D、30°2. 若a<b,则下列各式中一定成立的是( )A、﹣a<﹣b B、2a>2b C、a﹣1<b﹣1 D、ac2<bc23. 对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )A、∠1=50°,∠2=40° B、∠1=50°,∠2=50° C、∠1=∠2=45° D、∠1=40°,∠2=40°4. 如图,是一台自动测温记录仪的图象,它反映了嵊州市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
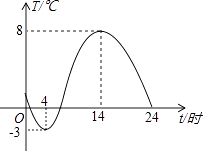 A、凌晨4时气温最低为﹣3℃ B、从0时至14时,气温随时间增长而上升 C、14时气温最高为8℃ D、从14时至24时,气温随时间增长而下降5. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
A、凌晨4时气温最低为﹣3℃ B、从0时至14时,气温随时间增长而上升 C、14时气温最高为8℃ D、从14时至24时,气温随时间增长而下降5. 如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( ) A、1个 B、2个 C、3个 D、4个6. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
A、1个 B、2个 C、3个 D、4个6. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、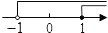 B、
B、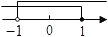 C、
C、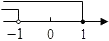 D、
D、 7. 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
7. 如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )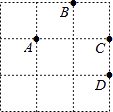 A、A点 B、B点 C、C点 D、D点8. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )
A、A点 B、B点 C、C点 D、D点8. 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=( )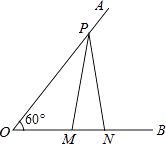 A、3 B、4 C、5 D、69. 运算与推理以下是甲、乙两人得到 + > 的推理过程:(甲)因为 > =3, > =2,所以 + >3+2=5.又 = < =5,所以 + > .(乙)作一个直角三角形,两直角边长分别为 , .利用勾股定理得斜边长的平方为 ,所以 + > .对于两个人的推理,下列说法中正确的是( )A、两人都正确 B、两人都错误 C、甲正确,乙错误 D、甲错误,乙正确10.
A、3 B、4 C、5 D、69. 运算与推理以下是甲、乙两人得到 + > 的推理过程:(甲)因为 > =3, > =2,所以 + >3+2=5.又 = < =5,所以 + > .(乙)作一个直角三角形,两直角边长分别为 , .利用勾股定理得斜边长的平方为 ,所以 + > .对于两个人的推理,下列说法中正确的是( )A、两人都正确 B、两人都错误 C、甲正确,乙错误 D、甲错误,乙正确10.如图,函数y=mx﹣4m(m是常数,且m≠0)的图象分别交x轴、y轴于点M,N,线段MN上两点A,B(点B在点A的右侧),作AA1⊥x轴,BB1⊥x轴,且垂足分别为A1 , B1 , 若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( )
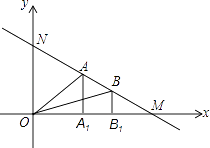 A、S1>S2 B、S1=S2 C、S1<S2 D、不确定的
A、S1>S2 B、S1=S2 C、S1<S2 D、不确定的二、填空题
-
11. 函数y= 中自变量x的取值范围是12. 命题“两直线平行,同位角相等.”的逆命题是 .13. 不等式3x﹣6<4x﹣2的最小整数解是 .14. 如图是一次函数的y=kx+b图象,则关于x的不等式kx+b>0的解集为 .
 15. 如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y= x上一点,则点B与其对应点B′间的距离为 .
15. 如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y= x上一点,则点B与其对应点B′间的距离为 .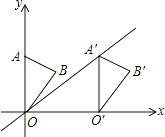 16. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x<13的解集为 .17. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省元.
16. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x<13的解集为 .17. 如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省元.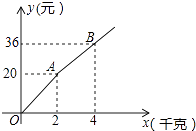 18. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AC=9,则CP的长为 .
18. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AC=9,则CP的长为 .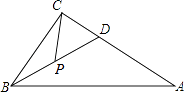 19. 按下面的程序计算,若开始输入的值x为正数,最后输出的结果为26,请写出符合条件的所有x的值 .
19. 按下面的程序计算,若开始输入的值x为正数,最后输出的结果为26,请写出符合条件的所有x的值 . 20. 如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 .
20. 如图,在直角坐标系中,点A的坐标是(0,2),点B是x轴上的一个动点,始终保持△ABC是等边三角形(点A、B、C按逆时针排列),当点B运动到原点O处时,则点C的坐标是 . 随着点B在x轴上移动,点C也随之移动,则点C移动所得图象的解析式是 .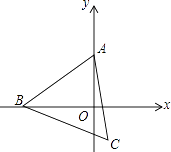
三、解答题
-
21. 解不等式(组)(1)、2x﹣7≤3(x﹣1)(2)、 并写出它的整数解.22. 如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:
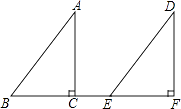 (1)、△ABC≌△DEF;(2)、AB∥DE.23. 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)、△ABC≌△DEF;(2)、AB∥DE.23. 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).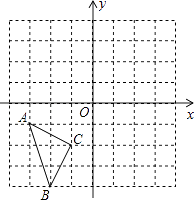
①将△ABC沿y轴正方向平移3个单位得到△A1B1C1 , 画出△A1B1C1 , 并写出点B1坐标;
②画出△A1B1C1关于y轴对称的△A2B2C2 , 并写出点C2的坐标.
24. 如图,△ABC中,∠C=90°,边AB的垂直平分线交AB、AC边分别为点D,点E,连结BE. (1)、若∠A=40°,求∠CBE的度数.(2)、若AB=10,BC=6,求△BCE的周长.25. 某厂每天只生产A、B两种型号的丝巾,共600条,A、B两种型号的丝巾每条的成本和利润如表,设每天生产A型号丝巾x条,该厂每天获利y元.
(1)、若∠A=40°,求∠CBE的度数.(2)、若AB=10,BC=6,求△BCE的周长.25. 某厂每天只生产A、B两种型号的丝巾,共600条,A、B两种型号的丝巾每条的成本和利润如表,设每天生产A型号丝巾x条,该厂每天获利y元.A
B
成本(元/条)
50
35
利润(元/条)
20
15
(1)、请写出y关于x的函数关系式;(2)、如果该厂每天至少投入成本26400元,那么每天至少获利多少元.26.已知:如图,△ABC中的顶点A、C分别在平面直角坐标系的x轴、y轴上,且∠ACB=90°,AC=2,BC=1,当点A从原点出发朝x轴的正方向运动,点C也随之在y轴上运动,当点C运动到原点时点A停止运动,连结OB.
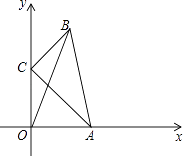 (1)、点A在原点时,求OB的长;(2)、当OA=OC时,求OB的长;(3)、在整个运动过程中,OB是否存在最大值?若存在,请你求出这个最大值;若不存在,请说明理由.
(1)、点A在原点时,求OB的长;(2)、当OA=OC时,求OB的长;(3)、在整个运动过程中,OB是否存在最大值?若存在,请你求出这个最大值;若不存在,请说明理由.四、附加题
-
27. 在平面直角坐标系中,我们不妨把纵坐标是横坐标的2倍的点称为“理想点”.例如点(﹣2,﹣4),(1,2),(3,6)…都是“理想点”,显然这样的“理想点”有无数多个.(1)、若点M(2,a)是“理想点”,且在正比例函数y=kx(k为常数,k≠0)图象上,求这个正比例函数的表达式.(2)、函数y=3mx﹣1(m为常数,且m≠0)的图象上存在“理想点”吗?若存在,请用含m的代数式表示出“理想点”的坐标;若不存在,请说明理由.28.
已知:等腰△ABC中,AB=AC,点D是直线AC上一动点,点E在BD的延长线上,且AB=AE,∠CAE的角平分线所在的直线交BE于F,连结CF.
 (1)、如图1,当点D在线段AC上时,求证:∠ABE=∠ACF;
(1)、如图1,当点D在线段AC上时,求证:∠ABE=∠ACF;
(2)、如图2,当∠ABC=60°且点D在线段AC上时,求证:AF+EF=FB.(提示:将线段FB拆分成两部分)(3)、①如图3,当∠ABC=45°其点D在线段AC上时,线段AF、EF、FB仍有(2)中的结论吗?若有,加以证明;
若没有,则有怎样的数量关系,直接写出答案即可.
②如图4,当∠ABC=45°且点D在CA的延长线时,请你按题意将图形补充完成.并直接写出线段AF、EF、FB的数量关系.
