2015-2016学年浙江省宁波市江北区九年级上学期期末数学试卷
试卷更新日期:2017-01-03 类型:期末考试
一、选择题
-
1. 若3x=2y,则x:y的值为( )A、2:3 B、3:2 C、3:5 D、2:52. 如果∠A是锐角,且sinA=cosA,那么∠A=( )A、30° B、45° C、60° D、90°3. 圆锥的母线长为4,侧面积为12π,则底面半径为( )A、6 B、5 C、4 D、34. 一个袋子中有7只黑球,6只黄球,5只白球,一次性取出12只球,其中出现黑球是( )A、不可能事件 B、必然事件 C、随机事件 D、以上说法均不对5. 下列函数中有最小值的是( )A、y=2x﹣1 B、y=﹣ C、y=2x2+3x D、y=﹣x2+16. 如果用
 表示1个立方体,用
表示1个立方体,用  表示两个立方体叠加,用
表示两个立方体叠加,用  表示三个立方体叠加,那么下图由6个立方体叠成的几何体的主视图是( )
表示三个立方体叠加,那么下图由6个立方体叠成的几何体的主视图是( )  A、
A、 B、
B、 C、
C、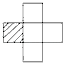 D、
D、 7. ⊙O内有一点P,过点P的所有弦中,最长的为10,最短的为8,则OP的长为( )A、6 B、5 C、4 D、38. 下列m的取值中,能使抛物线y=x2+(2m﹣4)x+m﹣1顶点在第三象限的是( )A、4 B、3 C、2 D、19. 四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( )
7. ⊙O内有一点P,过点P的所有弦中,最长的为10,最短的为8,则OP的长为( )A、6 B、5 C、4 D、38. 下列m的取值中,能使抛物线y=x2+(2m﹣4)x+m﹣1顶点在第三象限的是( )A、4 B、3 C、2 D、19. 四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图.则在字母L,K,C的投影中,与字母N属同一种投影的有( ) A、L,K B、C C、K D、L,K,C10. 如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( )
A、L,K B、C C、K D、L,K,C10. 如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( )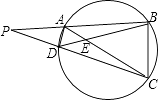 A、2对 B、3对 C、4对 D、5对11. 如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足 = ,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:
A、2对 B、3对 C、4对 D、5对11. 如图,AB是⊙O的直径,弦CD⊥AB于点G.点F是CD上一点,且满足 = ,连接AF并延长交⊙0于点E.连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E= ;④S△DEF=4 .
其中正确的是( )
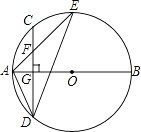 A、①②④ B、①②③ C、②③④ D、①③④12. 如图,在平面直角坐标系中,⊙P与y轴相切,交直线y=x于A,B两点,已知圆心P的坐标为(2,a)(a>2),AB=2 ,则a的值为( )
A、①②④ B、①②③ C、②③④ D、①③④12. 如图,在平面直角坐标系中,⊙P与y轴相切,交直线y=x于A,B两点,已知圆心P的坐标为(2,a)(a>2),AB=2 ,则a的值为( )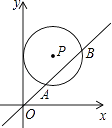 A、4 B、2+ C、 D、
A、4 B、2+ C、 D、二、填空题
-
13. 从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.1).
14. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),如果AB的长度为10cm,那么PB的长度为 cm. 15. 如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为 .
15. 如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为 .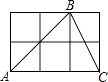 16. 如图,将一段12cm长的管道竖直置于地面,并在上面放置一个半径为5cm的小球,放置完毕以后小球顶端距离地面20cm,则该管道的直径AB为 .
16. 如图,将一段12cm长的管道竖直置于地面,并在上面放置一个半径为5cm的小球,放置完毕以后小球顶端距离地面20cm,则该管道的直径AB为 .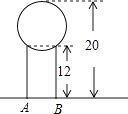 17. 如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为 cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
17. 如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合,OB与尺上沿的交点B在尺上的读数恰为2cm.若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数约为 cm.(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)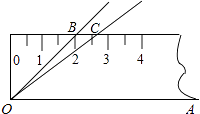 18. 如图,过y轴上一点P(0,1)作平行于x轴的直线PB,分别交函数y1=x2(x≥0)与y2= (x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016=
18. 如图,过y轴上一点P(0,1)作平行于x轴的直线PB,分别交函数y1=x2(x≥0)与y2= (x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016=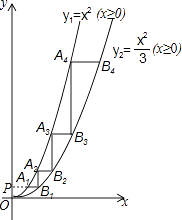
三、解答题
-
19. 计算:2cos30°+| ﹣2|+(2016﹣π)0﹣( )﹣1 .20. 如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,求S四边形DFGE:S四边形FBCG的值.
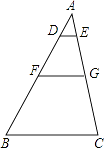 21. 如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子如图所示,已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度.(即AB的值)
21. 如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子如图所示,已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度.(即AB的值) 22. 如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.
22. 如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE.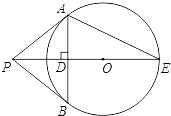 (1)、求证:PA是⊙O的切线;(2)、如果OD=3,tan∠AEP= ,求⊙O的半径.23. 甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.(1)、若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?(2)、若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?请说明理由.24. 某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量与销售单价基本满足一次函数关系,并且当销售单价为26元时,每天销售量28台;当销售单价为32元时,每天销售量16台,设台灯的销售单价为x(元),每天的销售量为y(台).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?(3)、若该商场每天想获得150元的利润,在保证销售量尽可能大的前提下,应将销售单价定为多少元?25.
(1)、求证:PA是⊙O的切线;(2)、如果OD=3,tan∠AEP= ,求⊙O的半径.23. 甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.(1)、若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?(2)、若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?请说明理由.24. 某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量与销售单价基本满足一次函数关系,并且当销售单价为26元时,每天销售量28台;当销售单价为32元时,每天销售量16台,设台灯的销售单价为x(元),每天的销售量为y(台).(1)、求y与x之间的函数关系式;(2)、当销售单价定为多少元时,每天的利润最大?最大利润是多少?(3)、若该商场每天想获得150元的利润,在保证销售量尽可能大的前提下,应将销售单价定为多少元?25.由若干边长为1的小正方形拼成一系列“L”形图案(如图1).
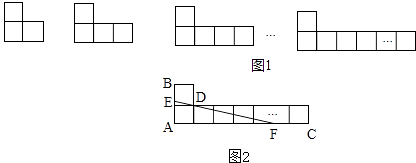 (1)、当“L”形由7个正方形组成时,其周长为;(2)、如图2,过格点D作直线EF,分别交AB,AC于点E,F.
(1)、当“L”形由7个正方形组成时,其周长为;(2)、如图2,过格点D作直线EF,分别交AB,AC于点E,F.①试说明AE•AF=AE+AF;
②若“L”形由n个正方形组成时,EF将“L”形分割开,直线上方的面积为整个“L”形面积的一半,试求n的取值范围以及此时线段EF的长.
26.已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO= ,以线段BC为直径作⊙M交直线AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+c,直线l与抛物线和⊙M的另一个交点分别是E,F.
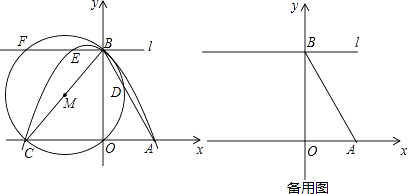 (1)、求B点坐标;(2)、用含m的式子表示抛物线的对称轴;(3)、线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.(4)、是否存在点C(m,0),使得BD= AB?若存在,求出此时m的值;若不存在,说明理由.
(1)、求B点坐标;(2)、用含m的式子表示抛物线的对称轴;(3)、线段EF的长是否为定值?如果是,求出EF的长;如果不是,说明理由.(4)、是否存在点C(m,0),使得BD= AB?若存在,求出此时m的值;若不存在,说明理由.