辽宁省朝阳市建平县2017-2018学年八年级上学期数学期末考试试卷
试卷更新日期:2018-06-04 类型:期末考试
一、单选题
-
1. 的平方根是( )A、9 B、±9 C、±3 D、32. 下列数据中不能作为直角三角形的三边长是( )A、1、1、 B、5、12、13 C、3、5、7 D、6、8、103. 在直角坐标系中,点M(1,2)关于x轴对称的点的坐标为( )A、(-1,2) B、(2,-1) C、(-1,-2) D、(1,-2)4. 如图,下列条件不能判断直线a∥b的是( )
 A、∠1=∠4 B、∠3=∠5 C、∠2+∠5=180° D、∠2+∠4=180°5. 下列四个命题中,真命题有( )
A、∠1=∠4 B、∠3=∠5 C、∠2+∠5=180° D、∠2+∠4=180°5. 下列四个命题中,真命题有( )①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③三角形的一个外角大于任何一个内角.
④如果x2>0,那么x>0.
A、1个 B、2个 C、3个 D、4个6. 已知小华上学期语文、数学、英语三科平均分为92分,他记得语文得了88分,英语得了95分,但他把数学成绩忘记了,你能告诉他应该是以下哪个分数吗?( )A、93 B、95 C、94 D、967. 如果 ,那么yx的算术平方根是( )A、2 B、3 C、9 D、±38. 设M= ,其中a=3,b=2,则M的值为( )A、2 B、-2 C、1 D、-19. 已知函数y=kx+b的图象如图所示,则函数y=-bx+k的图象大致是( )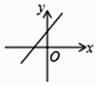 A、
A、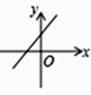 B、
B、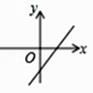 C、
C、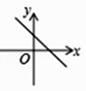 D、
D、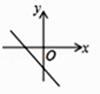 10. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( )
10. 如图,一个工人拿一个2.5米长的梯子,底端A放在距离墙根C点0.7米处,另一头B点靠墙,如果梯子的顶部下滑0.4米,梯子的底部向外滑多少米?( ) A、0.4 B、0.6 C、0.7 D、0.8
A、0.4 B、0.6 C、0.7 D、0.8二、填空题
-
11. 已知一组数据1,2,3,5,x,它的平均数是3,则这组数据的方差是 .12. 当m=时,函数y=(2m-1)x3m-2是正比例函数.13. 在y轴上,位于原点的下方,且距离原点4个单位长度的点的坐标是 .14. 如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组 的解是 .
 15. 如图,BD与CD分别平分∠ABC,∠ACB的外角∠EBC,∠FCB,若∠A=80°,则∠BDC= .
15. 如图,BD与CD分别平分∠ABC,∠ACB的外角∠EBC,∠FCB,若∠A=80°,则∠BDC= .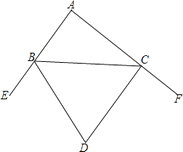 16. 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 .
16. 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 .
三、解答题
-
17. 计算:(1)、(2)、( -π)0- +(-1)2017 .18. 解方程组(1)、 ,(2)、 .19. 在边长为1的小正方形网格中,△AOB的顶点均在格点上.
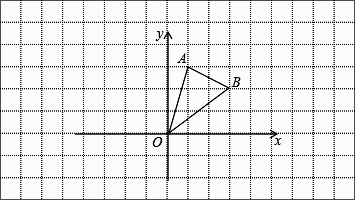 (1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;(3)、在(2)的条件下,A1的坐标为 .20. 某校八年级一班20名女生某次体育测试的成绩统计如下:
(1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;(3)、在(2)的条件下,A1的坐标为 .20. 某校八年级一班20名女生某次体育测试的成绩统计如下:成绩(分)
60
70
80
90
100
人数(人)
1
5
x
y
2
(1)、如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)、在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求 的值.21. 电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: (1)、分别写出当0≤x≤100和x>100时,y与x的函数关系式(2)、利用函数关系式,说明电力公司采取的收费标准(3)、若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?22. 甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?23. 如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求:
(1)、分别写出当0≤x≤100和x>100时,y与x的函数关系式(2)、利用函数关系式,说明电力公司采取的收费标准(3)、若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?22. 甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?23. 如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合,若长方形的长BC为8,宽AB为4,求: (1)、DE的长;
(1)、DE的长;
(2)、求阴影部分△GED的面积.24. 如图,点D,E分别在AB,AC上,DE∥BC,F是AD上一点,FE的延长线交BC的延长线于点G.求证: (1)、∠EGH>∠ADE;(2)、∠EGH=∠ADE+∠A+∠AEF.25. 如图,直线L:y=- x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动.
(1)、∠EGH>∠ADE;(2)、∠EGH=∠ADE+∠A+∠AEF.25. 如图,直线L:y=- x+2与x轴、y轴分别交于A、B两点,在y轴上有一点N(0,4),动点M从A点以每秒1个单位的速度匀速沿x轴向左移动. (1)、点A的坐标:;点B的坐标:;(2)、求△NOM的面积S与M的移动时间t之间的函数关系式;
(1)、点A的坐标:;点B的坐标:;(2)、求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)、在y轴右边,当t为何值时,△NOM≌△AOB,求出此时点M的坐标;
(4)、在(3)的条件下,若点G是线段ON上一点,连结MG,△MGN沿MG折叠,点N恰好落在x轴上的点H处,求点G的坐标.