辽宁省大连市中山区2017-2018学年七年级上学期数学期末考试试卷

试卷更新日期：2018-06-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中比1大的数是（）

A、2 B、0 C、-1 D、-3

查看试题解析
2. 下列图形中，不是三棱柱的表面展开图的是（）

A、 B、 C、 D、

查看试题解析
3. “犯我中华者，虽远必诛”爱国题材影片《战狼2》的票房喜获丰收，高达56.7亿元，把数56.7亿用科学记数法表示为（）

A、0.567×10¹⁰ B、56.7×10⁸ C、5.67×10⁹ D、5.67×10¹⁰

查看试题解析
4. 下列利用等式的性质，错误的是（）

A、由a=b，得到1-a=1-b B、由 $\frac{a}{2} = \frac{b}{2}$ ，得到a=b C、由a=b，得到ac=bc D、由ac=bc，得到a=b

查看试题解析
5. 单项式-2xy³的系数和次数分别是（）

A、-2，4 B、4，-2 C、-2，3 D、3，-2

查看试题解析
6. a，b是有理数，它们在数轴上的对应点的位置如图所示，把a，-a，b，-b按照从小到大的顺序排列（）

A、-b＜-a＜a＜b B、-a＜-b＜a＜b C、-b＜a＜-a＜b D、-b＜b＜-a＜a

查看试题解析
7. 如图，在直线l上顺次取A、B、C三点，使得AB=5cm，BC=3cm，如果O是线段AC的中点，那么线段OB长为（）

A、1cm B、1.5cm C、2cm D、4cm

查看试题解析
8. 一商店店主在某一时间内以150元的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%，则该店主在这两件衣服的交易中（）

A、赚了20元 B、赔了20元 C、不赔不赚 D、赚了25元

查看试题解析

二、填空题

9. 计算2×3+（-4）的结果为．

查看试题解析
10. 数轴是上点A、点B表示的数分别是-1和3，则点A、点B之间的距离是．

查看试题解析
11. 计算：3a-（2a-1）= ．

查看试题解析
12. 已知∠α的补角是它的3倍，则∠α= ．

查看试题解析
13. 关于x的方程x-3=kx+1的解是x=-8，则k= ．

查看试题解析
14. 如图，OB是∠AOC的平分线，OD是∠COE的平分线，如果∠AOE=140°，∠COD=30°，则∠AOB=°．

查看试题解析
15. 若x²+x+1的值是4，则3x²+3x+6的值是．

查看试题解析
16. 把一些图书分给某班学生阅读，若每人分3本，则剩余20本；若每人分4本，则还缺25本．这个班有多少学生？设这个班有x名学生，则由题意可列方程．

查看试题解析

三、解答题

17. 计算：

(1)、12+（-7）-（-15）

(2)、4+（-2）³×5-（-0.28）÷4．

查看试题解析
18. 已知A、B、C、D是同一平面内的四点，根据下列要求画图：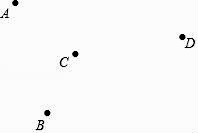

(1)、连接BD；

(2)、连接AC，并延长AC与BD相交于点E；

(3)、画射线DA．

查看试题解析
19. 解下列方程：

(1)、8x=-2（x+4）

(2)、 $\frac{x + 1}{2}$ =3- $\frac{x - 2}{4}$ ．

查看试题解析
20. 先化简，再求值：（2x²- $\frac{1}{2}$ +3x）-4（x-x²+ $\frac{1}{2}$ ），其中x=-1．

查看试题解析
21. 随着人们生活水平的提高，家用轿车越来越多地进入家庭．王先生家中买了一辆小轿车，他连续记录了7天中每天行驶的路程（如下表），以50km为标准，多于50km的记为“+”，不足50km的记为“-”，刚好50km的记为“0”．

第一天
第二天
第三天
第四天
第五天
第六天
第七天
路程（km）
-8
-11
-14
0
-16
+41
+15

(1)、王先生这七天中平均每天驾车行驶多少千米？

(2)、若每行驶1km需用汽油0.1升，汽油价格为6.5元/升，则王先生家一个月（按30天计）的汽油费用是多少元？

查看试题解析
22. 一套仪器由一个A部件和三个B部件构成，用1m³钢材可做40个A部件或240个B部件，现要用6m³钢材制作这种仪器，为使所做的A部件和B部件刚好配套，则做A部件和B部件的钢材各需多少m³？

查看试题解析
23. 观察下面三行数：
-2，4，-8，16，-32，…
-1，5，-7，17，-31，…
-4，8，-16，32，-64，…

(1)、第一行的第n个数是；（n为正整数）

(2)、第二行的第6个数是，第三行的第7个数是；

(3)、取每一行的第k个数，这三个数的和能否是-511？若能，求出k的值，若不能，请说明理由．

查看试题解析
24. 如图1，∠AOB=120°，∠COE=60°，OF平分∠AOE

(1)、若∠COF=20°，则∠BOE=°

(2)、将∠COE绕点O旋转至如图2位置，求∠BOE和∠COF的数量关系

(3)、在（2）的条件下，在∠BOE内部是否存在射线OD，使∠DOF=3∠DOE，且∠BOD=70°？若存在，求 $\frac{∠ DOF}{∠ C O F}$ 的值，若不存在，请说明理由．

查看试题解析
25. 如图，某景区内的环形路是边长为1200米的正方形ABCD，现有1号、2号两辆游览车分别从出口A和景点C同时出发，1号车沿A→B→C→D→A路线、2号车沿C→B→A→D→C路线连续循环行驶，供游客随时免费乘车（上、下车的时间忽略不计），两车速度均为300米/分．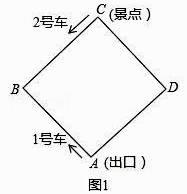

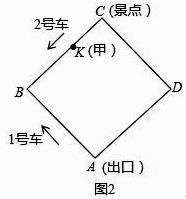(1)、如图1，设行驶时间为t分（0≤t≤8）
①1号车、2号车离出口A的路程分别为 ▲ 米， ▲ 米；（用含t的代数式表示）
②当两车相距的路程是600米时，求t的值；

(2)、如图2，游客甲在BC上的一点K（不与点B、C重合）处候车，准备乘车到出口A，设CK=x米．
情况一：若他刚好错过2号车，则他等候并搭乘即将到来的1号车；
情况二：若他刚好错过1号车，则他等候并搭乘即将到来的2号车．
请判断游客甲在哪种情况下乘车到出口A用时较多？（含候车时间）

查看试题解析
26. 如图，点B、C是线段AD上的两点，点M和点N分别在线段AB和线段CD上．

(1)、当AD=8，MN=6，AM=BM，CN=DN时，BC=；

(2)、若AD=a，MN=b
①当AM=2BM，DN=2CN时，求BC的长度（用含a和b的代数式表示）
②当AM=nBM，DN=nCN（n是正整数）时，直接写出BC= ．（用含a、b、n的代数式表示）

查看试题解析

	第一天	第二天	第三天	第四天	第五天	第六天	第七天
路程（km）	-8	-11	-14	0	-16	+41	+15