辽宁省朝阳市建平县2017-2018学年九年级上学期数学期末考试试卷

试卷更新日期：2018-06-04 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程x²-8x-2=0，配方的结果是（）

A、（x+4）²=18 B、（x+4）²=14 C、（x-4）²=18 D、（x-4）²=14

查看试题解析
2. 若反比例函数y= $\frac{k}{x}$ 图象经过点（5，-1），该函数图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
3. 如图所示的圆柱形茶叶筒的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 菱形 $O A C B$ 在平面直角坐标系中的位置如图所示，点 $C$ 的坐标是(6，0)，点 $A$ 的纵坐标是1，则点 $B$ 的坐标是（）

A、(3，1) B、(1，－3) C、(3，－1) D、(1，3)

查看试题解析
5. 以正方形ABCD两条对角线的交点O为坐标原点，建立如图所示的平面直角坐标系，双曲线y= $\frac{3}{x}$ 经过点D，则正方形ABCD的面积是（）

A、10 B、11 C、12 D、13

查看试题解析
6. 关于x的一元二次方程（m-1）x²+5x+m²-3m+2=0的常数项是0，则m的值（）

A、1 B、1或2 C、2 D、±1

查看试题解析
7. 如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（-4，4），（2，1），则位似中心的坐标为（）

A、（0，3） B、（0，2.5） C、（0，2） D、（0，1.5）

查看试题解析
8. 关于x的方程x²－mx－1＝0根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
9. 已知一次函数y=mx+n与反比例函数y= $\frac{n - m}{x}$ 其中m、n为常数，且mn＜0，则它们在同一坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 下列命题正确的是（）

A、对角线互相垂直平分且相等的四边形是正方形 B、对角线相等的四边形是矩形 C、一组对边相等，另一组对边平行的四边形是平行四边形 D、对角线互相垂直的四边形是菱形

查看试题解析

二、填空题

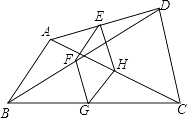
11. 在一个不透明的口袋内放入红球8个，黑球4个，黄球n个，这些球除颜色外无任何差别，摇匀后随机摸出一个恰好是黄球的概率为 $\frac{1}{5}$ ，则放入口袋中的黄球个数是.

查看试题解析
12. 如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，当四边形ABCD的边至少满足条件时，四边形EFGH是菱形．

查看试题解析
13. 如图，把一张矩形纸片ABCD按如图方式折叠，使顶点B和点D重合，折痕为EF，若AB=3cm，BC=4cm.则线段EF=cm.

查看试题解析
14. 如图，在四个小正方体搭成的几何体中，每个小正方体的棱长都是1，则该几何体的三视图的面积之和是.

查看试题解析
15. 如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB=1.5m，CD=4.5m，点P到CD的距离为2.7m，则AB与CD间的距离是m.

查看试题解析
16. 如图，在反比例函数y＝ $\frac{2}{x}$ (x>0)的图象上，有点P₁、P₂、P₃、P₄ ，它们的横坐标依次为1、2、3、4.分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次为S₁、S₂、S₃ ，则S₁＋S₂＋S₃＝.

查看试题解析

三、解答题

17. 解下列方程：

(1)、x²-8x+1=0（配方法）；

(2)、3x（x-1）=2-2x.

查看试题解析
18. 画出下列组合体的三视图.

查看试题解析
19. 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）.

(1)、△ABC向下平移4个单位长度得到的△A₁B₁C₁ ，点C₁的坐标是；

(2)、以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是；（画出图形）

(3)、△A₂B₂C₂的面积是平方单位.

查看试题解析
20. 在学校组织的朗诵比赛中，甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛，抽签规则是：在3个相同的标签上分别标注字母A、B、C，各代表1篇文章，一名学生随机抽取一个标签后放回，另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果，并求甲、乙抽中同一篇文章的概率.

查看试题解析
21. 某花店第一次购进甲、乙两种多肉植物共300株，甲种多肉植物每株的成本4元，售价为8元；乙种多肉植物每株成本价为6元，售价为10元

(1)、若第一次购进多肉植物的总金额为1400元，则购进甲种多肉植物多少株？

(2)、多肉植物一经上市，十分抢手，花店决定第二次购进甲乙两种多肉植物，它们的进价不变.甲种多肉植物的进货量在第一次进货量的基础上增加了2m%，售价也提高了m%，乙种多肉植物的售价和进货量不变，但是由于乙种多肉植物的耐热性不强，导致销售完之前它的成活率为90%，结果第二次共获利2100元，求m的值.

查看试题解析
22. 如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG.

(1)、写出线段AG，GE，GF长度之间的数量关系，并说明理由；

(2)、若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长.

查看试题解析
23. 如图，在矩形ABCD中，E，F分别为边AD，BC上的点，AE=CF，对角线AC平分∠ECF.

(1)、求证：四边形AECF为菱形.

(2)、已知AB=4，BC=8，求菱形AECF的面积.

查看试题解析
24. 直线y=kx+b与反比例函数y= $\frac{6}{x}$ （x＞0）的图象分别交于点 A（m，3）和点B（6，n），与坐标轴分别交于点C和点D.

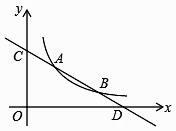(1)、求直线AB的解析式；

(2)、若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标.

查看试题解析
25. 如图，在直角坐标系中，Rt△ABC的直角边AC在x轴上，∠ACB=90°，AC=1，反比例函数y= $\frac{k}{x}$ （k＞0）的图象经过BC边的中点D（3，1）.

(1)、求这个反比例函数的表达式；

(2)、若△ABC与△EFG成中心对称，且△EFG的边FG在y轴的正半轴上，点E在这个函数的图象上.
①求OF的长；
②连接AF，BE，证明四边形ABEF是正方形.

查看试题解析