2015-2016学年浙江省金华市婺城区九年级上学期期末数学试卷

试卷更新日期：2017-01-03 类型：期末考试

进入出卷网下载

一、选择题

1. ﹣2016的相反数是（）

A、 $- \frac{1}{2016}$ B、 $\frac{1}{2016}$ C、6102 D、2016

查看试题解析
2. 四边形的内角和为（）

A、90° B、180° C、360° D、720°

查看试题解析
3. 已知 $\frac{b}{a}$ = $\frac{2}{3}$ ，则 $\frac{a}{a + b}$ 的值是（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{5}{3}$ D、 $\frac{5}{2}$

查看试题解析
4. 将抛物线y=3x²向上平移1个单位，得到抛物线（）

A、y=3（x﹣1）² B、y=3（x+1）² C、y=3x²﹣1 D、y=3x²+1

查看试题解析
5. 在水平的讲台上放置圆柱形水杯和长方体形粉笔盒（如图），则它的主视图是（）

A、图① B、图② C、图③ D、图④

查看试题解析
6. 在Rt△ABC中，∠ACB=90°，BC=1，AB=2，则sinA的值为（）

A、 $\frac{1}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 已知半径为3的圆⊙O外有一条直线l，已知⊙O与直线l相切，则圆心到直线l的距离为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 在一个不透明的袋中装着3个红球和1个黄球，它们只有颜色上的区别，随机从袋中摸出2个小球，两球恰好是一个黄球和一个红球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
9. 如果正比例函数y=ax（a≠0）与反比例函数y= $\frac{b}{x}$ （b≠0 ）的图象有两个交点，其中一个交点的坐标为（﹣3，﹣2），那么另一个交点的坐标为（）

A、（2，3） B、（3，﹣2） C、（﹣2，3） D、（3，2）

查看试题解析
10.
如图1，E为矩形ABCD边AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是1cm/s．若P，Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm²）．已知y与t的函数图象如图2，则下列结论错误的是（）

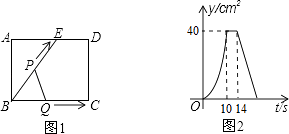A、AE=6cm B、sin∠EBC= $\frac{4}{5}$ C、当0＜t≤10时，y= $\frac{2}{5}$ t² D、当t=12s时，△PBQ是等腰三角形

查看试题解析

二、填空题

11. 函数 $y = \frac{1}{x - 1}$ 中，自变量x的取值范围是．

查看试题解析
12. 因式分解：ab²﹣64a=

查看试题解析
13. 扇形的半径为30cm，圆心角为120°，用它做成一个圆锥的侧面，若不计接缝和损耗，则圆锥底面半径为．

查看试题解析
14.
用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第n个图案中共有小三角形的个数是．

查看试题解析
15. 对任意两实数a、b，定义运算“*”如下： $a * b = {\begin{matrix} b^{a} (a \geq b) \\ b^{a} + b (a < b) \end{matrix}$ ．根据这个规则，则方程2*x=9的解为．

查看试题解析
16. 如图，梯形OABC中，BC∥AO，O（0，0），A（10，0），B（10，4），BC=2，G（t，0）是底边OA上的动点．

(1)、tan∠OAC= ．

(2)、边AB关于直线CG的对称线段为MN，若MN与△OAC的其中一边平行时，则t=

查看试题解析

三、解答题

17. 计算： ${(1 + \sqrt{2})}^{0} + {(\frac{1}{2})}^{- 1} + 2 \cdot \cos 30^{\circ} - | - \sqrt{3} |$ ．

查看试题解析
18. 已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．

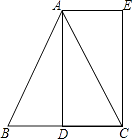(1)、求证：△ABD≌△CAE；

(2)、连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．

查看试题解析
19. 如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．
（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20）．

查看试题解析
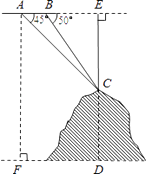20. 如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D=60°且AB=6，过O点作OE⊥AC，垂足为E．

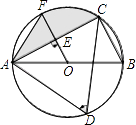(1)、求OE的长；

(2)、若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积S．

查看试题解析
21. 为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：（A组：x＜155； B组：155≤x＜160； C组：160≤x＜165； D组165≤x＜170；E组：x≥170）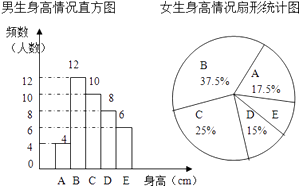
根据图表提供的信息，回答下列问题：

(1)、样本中，男生的身高众数在组，中位数在组．

(2)、样本中，女生的身高在E组的人数有人．

(3)、已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？

查看试题解析
22. 阅读下列材料：小华遇到这样一个问题：
已知：如图1，在△ABC中，三边的长分别为AB= $\sqrt{10}$ ，AC= $\sqrt{2}$ ，BC=2，求∠A的正切值．
小华是这样解决问题的：
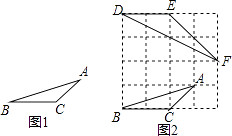
如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．

(1)、如图2，△DEF中与∠A相等的角为， ∠A的正切值为．

(2)、参考小华的方法请解决问题：若△LMN的三边分别为LM=2，MN=2 $\sqrt{2}$ ，LN=2 $\sqrt{5}$ ，求∠N的正切值．

查看试题解析
23. 某公司装修需用A型板材240块，B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm．现只能购得规格是150cm×30cm的标准板材．一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）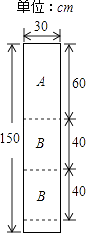

裁法一
裁法二
裁法三
A型板材块数
1
2
0
B型板材块数
2
m
n

(1)、上表中，m= ， n=；

(2)、若裁完剩余的部分可以拼接成A型或B型板材使用，则至少需要几张标准板材？

(3)、若裁完剩余的部分不能拼接成A型或B型板材使用，已知用170张标准板材，可以完成装修任务．请通过计算写出两种剪裁方案（要求：①其中一种方案三种剪裁方法都使用，另一种方案只用到两种剪裁方法；②每种方案需写出使用各种裁剪方法裁剪标准板的张数）．

查看试题解析
24.
在平面直角坐标系中，O是坐标原点，矩OABC的位置如图所示，点A，C的坐标分别为（10，0），（0，8），点P是y轴上的一个动点，将△OAP沿AP翻折得到：△O′AP，直线BC与直线O′P交于点E，与直线O′A交于点F．

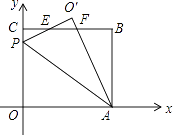(1)、当O′落在直线BC上时，求折痕AP的长．

(2)、当点P在y轴正半轴上时，若△PCE与△POA相似，求直线AP的解析式；

(3)、在点P的运动过程中，是否存在某一时刻，使得 $\frac{C E}{B C} = \frac{1}{5}$ ？若存在，求点P坐标；若不存在，请说明理由．

查看试题解析

	裁法一	裁法二	裁法三
A型板材块数	1	2	0
B型板材块数	2	m	n