辽宁省本溪市2015-2016学年九年级上学期数学期末考试试卷
试卷更新日期:2018-06-04 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果反比例函数y= 的图象经过点(-3,-4),那么函数的图象应在( )A、第一,三象限 B、第一,二象限 C、第二,四象限 D、第三,四象限3. 图中三视图所对应的直观图是( )
2. 如果反比例函数y= 的图象经过点(-3,-4),那么函数的图象应在( )A、第一,三象限 B、第一,二象限 C、第二,四象限 D、第三,四象限3. 图中三视图所对应的直观图是( )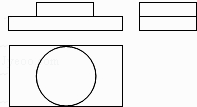 A、
A、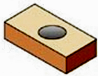 B、
B、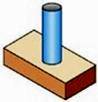 C、
C、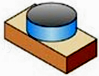 D、
D、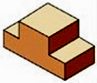 4. 若关于x的一元二次方程x2-2x-k=0有两个不相等的实数根,则实数k的取值范围是( )A、k>-1 B、k<1且k≠0 C、k≥-1且k≠0 D、k>-1且k≠05. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
4. 若关于x的一元二次方程x2-2x-k=0有两个不相等的实数根,则实数k的取值范围是( )A、k>-1 B、k<1且k≠0 C、k≥-1且k≠0 D、k>-1且k≠05. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形6. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形6. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为( )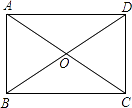 A、 cm B、2cm C、2 cm D、4cm7. 在函数y= (k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y18. 已知 =3,则 的值为( )A、 B、 C、 D、-9. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )
A、 cm B、2cm C、2 cm D、4cm7. 在函数y= (k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y18. 已知 =3,则 的值为( )A、 B、 C、 D、-9. 如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC相似的是( )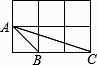 A、
A、 B、
B、 C、
C、 D、
D、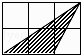 10.
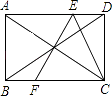
10.如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )
 A、5cm B、8cm C、9cm D、10cm
A、5cm B、8cm C、9cm D、10cm二、填空题
-
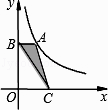
11. 如图,点A是反比例函数 (x>0)图象上任意一点,AB⊥y轴于B,点C是x轴上的动点,则△ABC的面积为 .
 12. 一药品售价100元,连续两次降价后的价格为81元,则平均每次降价的降价率是%.13. 已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为cm.
12. 一药品售价100元,连续两次降价后的价格为81元,则平均每次降价的降价率是%.13. 已知菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,则菱形的高AE为cm.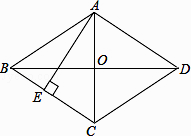 14. 已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6),直线y=mx+2将四边形ABCD分成面积相等的两部分,则m的值为 .15. 如图,△ABC的顶点是正方形网格的格点,则tanA的值为 .
14. 已知平面上四点A(0,0),B(10,0),C(10,6),D(0,6),直线y=mx+2将四边形ABCD分成面积相等的两部分,则m的值为 .15. 如图,△ABC的顶点是正方形网格的格点,则tanA的值为 .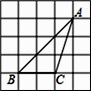 16. 如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y= (x>0)的图象上,则E点的坐标是 .
16. 如图,正方形OABC和正方形ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y= (x>0)的图象上,则E点的坐标是 .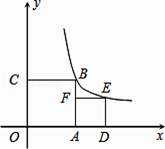 17. 对于正数x,规定f(x)= ,例如f(2)= ,f(3)= ,f( )= ,f( )= ,计算:f( )+f( )+f( )+…+f( )+f( )+f(1)+f(2)+f(3)+…+f(2014)+f(2015)+f(2016)的结果是 .
17. 对于正数x,规定f(x)= ,例如f(2)= ,f(3)= ,f( )= ,f( )= ,计算:f( )+f( )+f( )+…+f( )+f( )+f(1)+f(2)+f(3)+…+f(2014)+f(2015)+f(2016)的结果是 .
三、解答题
-
18.
(1)、(2)、x(x+3)=7(x+3)19. 在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.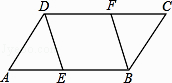 (1)、求证:△ADE≌△CBF;
(1)、求证:△ADE≌△CBF;
(2)、若DF=BF,求证:四边形DEBF为菱形.20. 为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.(1)、请用树形图法或列表法,表示某个同学抽签的各种可能情况.(2)、小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?21. 如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.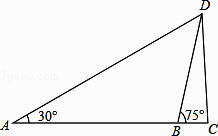 (1)、求点B到AD的距离;(2)、求塔高CD(结果用根号表示).22. 如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°求证:AG=FG.
(1)、求点B到AD的距离;(2)、求塔高CD(结果用根号表示).22. 如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°求证:AG=FG.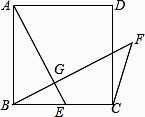 23. 直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y= (x<0)交于点A(-1,n).
23. 直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y= (x<0)交于点A(-1,n).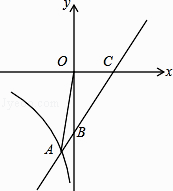 (1)、求直线与双曲线的解析式.(2)、连接OA,求∠OAB的正弦值.
(1)、求直线与双曲线的解析式.(2)、连接OA,求∠OAB的正弦值.
24. 把两块全等的直角三角形ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q. (1)、如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=;(2)、将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;(3)、在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)25. 如图,在平面直角坐标系中,直线l所在的直线的解析式为y= x,点B坐标为(10,0)过B做BC⊥直线l,垂足为C,点P从原点出发沿x轴方向向点B运动,速度为1单位/s,同时点Q从点B出发沿B→C→原点方向运动,速度为2个单位/s,当一个动点到达终点时,另一个动点也随之停止运动.
(1)、如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时,AP•CQ=;(2)、将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP•CQ的值是否改变?说明你的理由;(3)、在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图2,图3供解题用)25. 如图,在平面直角坐标系中,直线l所在的直线的解析式为y= x,点B坐标为(10,0)过B做BC⊥直线l,垂足为C,点P从原点出发沿x轴方向向点B运动,速度为1单位/s,同时点Q从点B出发沿B→C→原点方向运动,速度为2个单位/s,当一个动点到达终点时,另一个动点也随之停止运动.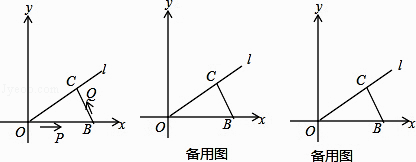 (1)、OC= , BC=;(2)、当t=5(s)时,试在直线PQ上确定一点M,使△BCM的周长最小,并求出该最小值;
(1)、OC= , BC=;(2)、当t=5(s)时,试在直线PQ上确定一点M,使△BCM的周长最小,并求出该最小值;
(3)、设点P的运动时间为t(s),△PBQ的面积为y,当△PBQ存在时,求y与t的函数关系式,并写出自变量t的取值范围.