辽宁大连市中山区2015-2016学年九年级上学期数学期末考试试卷

试卷更新日期：2018-06-04 类型：期末考试

进入出卷网下载

一、单选题

1. 已知四条线段满足a= $\frac{c d}{b}$ ，将它改写成为比例式，下面正确的是（　　）

A、 $\frac{a}{b}$ = $\frac{c}{d}$ B、 $\frac{a}{c}$ = $\frac{b}{d}$ C、 $\frac{a}{c}$ = $\frac{d}{b}$ D、 $\frac{a}{d}$ = $\frac{b}{c}$

查看试题解析
2. 二次函数y= $- 2 {(x - 1)}^{2} + 3$ 的图象的顶点坐标是（）.

A、（1，3） B、（-1，3） C、（1，-3） D、（-1，-3）

查看试题解析
3. 下列事件中，必然事件是（　　）

A、抛出一枚硬币，落地后正面向上 B、打开电视，正在播放广告 C、篮球队员在罚球线投篮一次，未投中 D、实心铁球投入水中会沉入水底

查看试题解析
4.
如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则∠ABD=（　　）

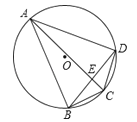A、∠ACD B、∠ADB C、∠AED D、∠ACB

查看试题解析
5. 用配方法解一元二次方程 $x^{2}$ -4x=5时，此方程可变形为（）.

A、 ${(x + 2)}^{2}$ =1 B、 ${(x - 2)}^{2}$ =1 C、 ${(x + 2)}^{2}$ =9 D、 ${(x - 2)}^{2}$ =9

查看试题解析
6. 若△ABC∽△A′B′C′，相似比为1：2，则△ABC与△A′B′C′的面积的比为（　　）

A、1：2 B、2：1 C、1：4 D、4：1

查看试题解析
7. 已知函数y= $x^{2}$ +2x-3，当x=m时，y＜0，则m的值可能是（）.

A、-4 B、0 C、2 D、3

查看试题解析
8. 一个圆锥的高为4cm，底面圆的半径为3cm，则这个圆锥的侧面积为（　　）

A、12πcm² B、15πcm² C、20πcm² D、30πcm²

查看试题解析

二、填空题

9. 方程 $x^{2}$ -4x+c=0有两个不相等的实数根，则c的取值范围是．

查看试题解析
10. 在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为m．

查看试题解析
11. 如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到 $△ O A_{1} B_{1}$ ，则∠ $A_{1} O B$ = ．

查看试题解析
12. 抽屉里放着黑、白两种颜色的袜子各1双(除颜色外其余都相同)，在看不到的情况下随机摸出两只袜子，它们恰好同色的概率是．

查看试题解析
13. 一元二次方程 $x^{2}$ +px-2=0的一个根为2，则p的值．

查看试题解析
14. 如图，在⊙O中，已知半径为5，弦AB的长为8，那么圆心O到AB的距离为．

查看试题解析
15. 如图，要使△ABC与△DBA相似，则只需添加一个适当的条件是（填一个即可）.

查看试题解析
16. 二次函数y= $a x^{2}$ +bx+c的图象如图所示，其对称轴与x轴交于点（-1，0），图象上有三个点分别为（2， $y_{1}$ ），（-3， $y_{2}$ ），（0， $y_{3}$ ），则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（用“＞”“＜”或“=”连接）．

查看试题解析

三、解答题

17. 解方程：

(1)、 $x^{2}$ -4x+1=0；

(2)、x（x-2）+x-2=0．

查看试题解析
18. 如图，△ABC的三个顶点都在格点上，每个小方格边长均为1个单位长度．

(1)、请你作出△ABC关于点O成中心对称的 $△ A_{1} B_{1} C_{1}$ （其中A的对称点是 $A_{1}$ ，B的对称点是 $B_{1}$ ，C的对称点是 $C_{1}$ ；

(2)、直接写出点 $B_{1}$ 、 $C_{1}$ 的坐标．

查看试题解析
19. 如图，四边形ABCD内接于⊙O，E为AB延长线上一点，若∠AOC=140°．求∠EBC的度数．

查看试题解析
20. 一只不透明的箱子里共有3个球，把它们的分别编号为1，2，3，这些球除编号不同外其余都相同，从箱子中随机摸出一个球，记录下编号后将它放回箱子，搅匀后再摸出一个球并记录下编号．

(1)、用树状图或列表法举出所有可能出现的结果；

(2)、求两次摸出的球都是编号为3的球的概率．

查看试题解析
21. 如图，Rt△ABC中，∠C=90°，AB=10，AC=8，E是AC上一点，AE=5，ED⊥AB于D．

(1)、求证：△ACB∽△ADE；

(2)、求AD的长度．

查看试题解析
22. 如图，进行绿地的长、宽各增加xm．

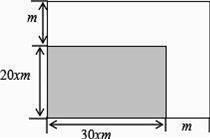(1)、写出扩充后的绿地的面积y（ $m^{2}$ ）与x（m）之间的函数关系式；

(2)、若扩充后的绿地面积y是原矩形面积的2倍，求x的值．

查看试题解析
23. 如图，AB是⊙O的直径，点C、D在⊙O上，且AC平分∠BAD，点E为AB的延长线上一点，且∠ECB=∠CAD．

(1)、①填空：∠ACB= ▲ ，理由是 ▲ ；
②求证：CE与⊙O相切；

(2)、若AB=6，CE=4，求AD的长．

查看试题解析
24. 如图1，在△ABC中，∠A=120°，AB=AC，点P、Q同时从点B出发，以相同的速度分别沿折线B→A→C、射线BC运动，连接PQ．当点P到达点C时，点P、Q同时停止运动．设BQ=x，△BPQ与△ABC重叠部分的面积为S．如图2是S关于x的函数图象（其中0≤x≤8，8＜x≤m，m＜x≤16时，函数的解析式不同）．

(1)、填空：m的值为；

(2)、求S关于x的函数关系式，并写出x的取值范围；

(3)、请直接写出△PCQ为等腰三角形时x的值．

查看试题解析
25. 如图（1），将线段AB绕点A逆时针旋转2α（0°＜α＜90°）至AC，P是过A，B，C的三点圆上任意一点．

(1)、当α=30°时，如图（1），求证：PC=PA+PB；

(2)、当α=45°时，如图（2），PA，PB，PC三条线段间是否还具有上述数量关系？若有，请说明理由；若不具有，请探索它们的数量关系．

查看试题解析
26. 如图，抛物线y= $a {(x - \sqrt{2} m)}^{2} - m$ .（其中m＞1）与其对称轴l相交于点P，与y轴相交于点A（0，m）．点A关于直线l的对称点为B，作BC⊥x轴于点C，连接PC、PB，与抛物线、x轴分别相交于点D、E，连接DE．将△PBC沿直线PB翻折，得到△PBC′．

(1)、该抛物线的解析式为；（用含m的式子表示）；

(2)、探究线段DE、BC的关系，并证明你的结论；

(3)、直接写出C′点的坐标（用含m的式子表示）．

查看试题解析