浙江省衢州市2018届数学中考一模试卷
试卷更新日期:2018-06-04 类型:中考模拟
一、单选题
-
1. 计算(﹣a2)5的结果是( )A、a7 B、﹣a7 C、a10 D、﹣a102. 下面是小林做的4道作业题:(1)2ab+3ab=5ab;(2)2ab﹣3ab=﹣ab;(3)2ab﹣3ab=6ab;(4)2ab÷3ab= .做对一题得2分,则他共得到( )A、2分 B、4分 C、6分 D、8分3. 已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组 的解的个数为( )
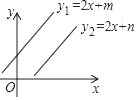 A、0个 B、1个 C、2个 D、无数个4.
A、0个 B、1个 C、2个 D、无数个4.抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
 A、20,20 B、30,20 C、30,30 D、20,305. 当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )
A、20,20 B、30,20 C、30,30 D、20,305. 当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )V(单位:m3)
1
1.5
2
2.5
3
P(单位:kPa)
96
64
48
38.4
32
A、P=96V B、P=﹣16V+112 C、P=16V2﹣96V+176 D、P=6. 如图,在射线OA,OB上分别截取OA1=OB1 , 连接A1B1 , 在B1A1 , B1B上分别截取B1A2=B1B2 , 连接A2B2 , …按此规律作下去,若∠A1B1O=α,则∠A10B10O=( ) A、 B、 C、 D、7. 已知抛物线c:y=x2+2x﹣3,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )A、将抛物线c沿x轴向右平移 个单位得到抛物线c′ B、将抛物线c沿x轴向右平移4个单位得到抛物线c′ C、将抛物线c沿x轴向右平移 个单位得到抛物线c′ D、将抛物线c沿x轴向右平移6个单位得到抛物线c′8. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①弧AB=弧CD;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
A、 B、 C、 D、7. 已知抛物线c:y=x2+2x﹣3,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )A、将抛物线c沿x轴向右平移 个单位得到抛物线c′ B、将抛物线c沿x轴向右平移4个单位得到抛物线c′ C、将抛物线c沿x轴向右平移 个单位得到抛物线c′ D、将抛物线c沿x轴向右平移6个单位得到抛物线c′8. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①弧AB=弧CD;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( ) A、1 B、2 C、3 D、49. 如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的度数为( )
A、1 B、2 C、3 D、49. 如图,在平行四边形ABCD中,E是边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的度数为( ) A、40° B、36° C、50° D、45°10. 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确结论的个数是( )
A、40° B、36° C、50° D、45°10. 如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= ,其中正确结论的个数是( ) A、1 B、2 C、3 D、411. AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为 .
A、1 B、2 C、3 D、411. AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为 .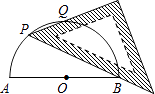
二、填空题
-
12. 从- ,0, ,π,3.5这五个数中,随机抽取一个,则抽到无理数的概率是 .13. 如图,反比例函数y= 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为 .
 14. 小菲受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作,请根据图中给出的信息,量筒中至少放入小球时有水溢出.
14. 小菲受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作,请根据图中给出的信息,量筒中至少放入小球时有水溢出. 15. 如图,点P为∠MON平分线OC上一点,以点P为顶点的∠APB两边分别与射线OM、ON相交于点A、B,如果∠APB在绕点P旋转时始终满足 ,我们就把∠APB叫做∠MON的关联角.如果∠MON=50°,∠APB是∠MON的关联角,那么∠APB的度数为 .
15. 如图,点P为∠MON平分线OC上一点,以点P为顶点的∠APB两边分别与射线OM、ON相交于点A、B,如果∠APB在绕点P旋转时始终满足 ,我们就把∠APB叫做∠MON的关联角.如果∠MON=50°,∠APB是∠MON的关联角,那么∠APB的度数为 .
 16. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.
16. 两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了m,恰好把水喷到F处进行灭火.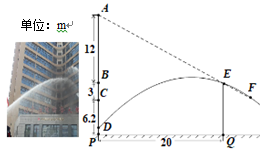
三、解答题
-
17. 计算
(1)、计算: ﹣2sin45°+(2﹣π)0﹣( )﹣1;(2)、先化简,再求值 •(a2﹣b2),其中a= ,b=﹣2 .18. 解分式方程:19. 某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下) (1)、写出D级学生的人数占全班总人数的百分比为 , C级学生所在的扇形圆心角的度数为;(2)、该班学生体育测试成绩的中位数落在等级内;(3)、若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?20. 小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.
(1)、写出D级学生的人数占全班总人数的百分比为 , C级学生所在的扇形圆心角的度数为;(2)、该班学生体育测试成绩的中位数落在等级内;(3)、若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?20. 小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角. (1)、填空:ADAC(填“>”,“<”,“=”).(2)、求旗杆AB的高度.
(1)、填空:ADAC(填“>”,“<”,“=”).(2)、求旗杆AB的高度.(参考数据: ≈1.41, ≈1.73,结果精确到0.1m).
21. 如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数 的图象交于点B、E. (1)、求反比例函数及直线BD的解析式;(2)、求点E的坐标.22. 在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)、求反比例函数及直线BD的解析式;(2)、求点E的坐标.22. 在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F. (1)、求证:AC是⊙O的切线;(2)、若BF=6,⊙O的半径为5,求CE的长.23. 如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)、求证:AC是⊙O的切线;(2)、若BF=6,⊙O的半径为5,求CE的长.23. 如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.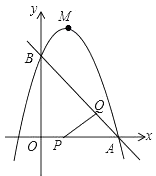
 (1)、求抛物线的解析式;(2)、当t为何值时,△APQ为直角三角形;(3)、过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.24. 在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC= ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)、求抛物线的解析式;(2)、当t为何值时,△APQ为直角三角形;(3)、过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.24. 在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC= ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.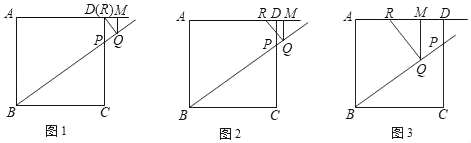 (1)、如图1,当点R与点D重合时,求PQ的长;(2)、如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)、如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.
(1)、如图1,当点R与点D重合时,求PQ的长;(2)、如图2,试探索: 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)、如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.