江苏省无锡市惠山区西漳镇2018届数学中考一模试卷
试卷更新日期:2018-06-04 类型:中考模拟
一、单选题
-
1. ﹣5的倒数是( )A、5 B、﹣5 C、 D、﹣2. 函数y= 中自变量x的取值范围是( )A、x>1 B、x≥1 C、x≤1 D、x≠13. 下列图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、x+x2=x3 B、2x-3x=-x C、(x2)3=x5 D、x6÷x3=x25. 分式方程 的解为( )A、x=0 B、x=3 C、x=5 D、x=96. 下列说法中,正确的是( )
4. 下列计算正确的是( )A、x+x2=x3 B、2x-3x=-x C、(x2)3=x5 D、x6÷x3=x25. 分式方程 的解为( )A、x=0 B、x=3 C、x=5 D、x=96. 下列说法中,正确的是( )
A、为检测我市正在销售的酸奶质量,应该采用抽样调查的方式 B、两名同学连续五次数学测试的平均分相同,方差较大的同学数学成绩更稳定 C、抛掷一个正方体骰子,点数为奇数的概率是 D、“打开电视,正在播放广告”是必然事件7. 如图是某几何体的三视图及相关数据,则该几何体的全面积是( ) A、15π B、24π C、20π D、10π8. 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ,E,F分别是AD,CD的中点,连接BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
A、15π B、24π C、20π D、10π8. 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 ,E,F分别是AD,CD的中点,连接BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( ) A、2 B、 C、 D、39. 如图,在△ABC中,D为AB边上一点,E为CD中点,AC= ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )
A、2 B、 C、 D、39. 如图,在△ABC中,D为AB边上一点,E为CD中点,AC= ,∠ABC=30°,∠A=∠BED=45°,则BD的长为( )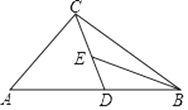 A、 B、 +1﹣ C、 ﹣ D、 ﹣110. 如图,△ABC为⊙O的内接三角形,BC=24 , ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )
A、 B、 +1﹣ C、 ﹣ D、 ﹣110. 如图,△ABC为⊙O的内接三角形,BC=24 , ,点D为弧BC上一动点,CE垂直直线OD于点E, 当点D由B点沿弧BC运动到点C时,点E经过的路径长为( )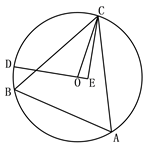 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 分解因式:x3﹣2x2+x= .12. 据统计,今年无锡 “古运河之光”旅游活动节期间,访问南长历史文化街区的国内外游客约908万人次,908万人次用科学记数法可表示为人次.13. 已知一元二次方程x2﹣3x﹣6=0有两个实数根x1、x2 , 直线l经过点A(x1+x2 , 0)、B(0,x1•x2),则直线l不经过第象限.14. “同位角相等”的逆命题是 .15. 如图,⊙O的直径AB与弦CD相交于点E,AB=5,AC=3,则tan∠ADC = .
 16. 已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为 .17. 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE= .
16. 已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为 .17. 如图,Rt△ABC中,∠BAC=90°,将△ABC绕点C逆时针旋转,旋转后的图形是△A′B′C,点A的对应点A′落在中线AD上,且点A′是△ABC的重心,A′B′与BC相交于点E,那么BE:CE= .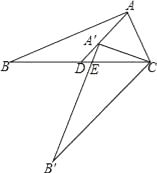 18. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1 , S2 , S3 , …,Sn , 则Sn的值为 (用含n的代数式表示,n为正整数).
18. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1 , S2 , S3 , …,Sn , 则Sn的值为 (用含n的代数式表示,n为正整数).
三、解答题
-
19. 计算
(1)、计算6sin60°﹣( )﹣2﹣(2)、化简:20. 解方程和不等式组
(1)、解方程:(2)、解不等式组:21. 已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. (1)、求证:△AOD ≌ △EOC;(2)、连接AC,DE,当∠B ∠AEB 等于多少度时,四边形ACED是正方形?请说明理由.
(1)、求证:△AOD ≌ △EOC;(2)、连接AC,DE,当∠B ∠AEB 等于多少度时,四边形ACED是正方形?请说明理由. 22. 初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
22. 初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题: (1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)、请将频数分布直方图补充完整;
(4)、如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
23. 为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4个不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.(1)、请用树形图法或列表法,表示某个同学抽签的各种可能情况.(2)、小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少?
24. 如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少? 25. 重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y= x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=- x+ (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:
25. 重庆市的重大惠民工程﹣﹣公租房建设已陆续竣工,计划10年内解决低收入人群的住房问题,前6年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y= x+5,(x单位:年,1≤x≤6且x为整数);后4年,每年竣工投入使用的公租房面积y(单位:百万平方米),与时间x的关系是y=- x+ (x单位:年,7≤x≤10且x为整数).假设每年的公租房全部出租完.另外,随着物价上涨等因素的影响,每年的租金也随之上调,预计,第x年投入使用的公租房的租金z(单位:元/m2)与时间x(单位:年,1≤x≤10且x为整数)满足一次函数关系如下表:z(元/m2)
50
52
54
56
58
…
x(年)
1
2
3
4
5
…
(1)、求出z与x的函数关系式;(2)、求政府在第几年投入的公租房收取的租金最多,最多为多少百万元;
(3)、若第6年竣工投入使用的公租房可解决20万人的住房问题,政府计划在第10年投入的公租房总面积不变的情况下,要让人均住房面积比第6年人均住房面积提高a%,这样可解决住房的人数将比第6年减少1.35a%,求a的值.(参考数据: , , )
26. 已知A(2,0),B(6,0),CB⊥x轴于点B,连接AC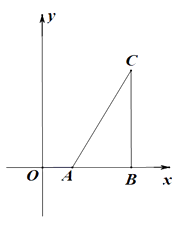
画图操作:
(1)、在y正半轴上求作点P,使得∠APB=∠ACB(尺规作图,保留作图痕迹)(2)、在(1)的条件下,①若tan∠APB ,求点P的坐标。
②当点P的坐标为 时,∠APB最大
(3)、若在直线y x+4上存在点P,使得∠APB最大,求点P的坐标 27. 如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6).
27. 如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6). (1)、求抛物线的解析式;(2)、如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(1)、求抛物线的解析式;(2)、如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(3)、如果点M是直线BC上的动点,是否存在一个点M,使△ABM中有一个角为45°?如果存在,直接写出所有满足条件的M点坐标;如果不存在,请说明理由.28. 问题提出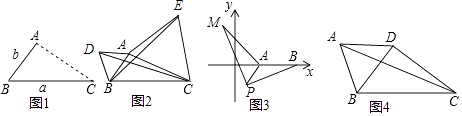 (1)、如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示).(2)、点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.(3)、如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(1)、如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示).(2)、点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.(3)、如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(4)、如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC= ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.