2015-2016学年浙江省金华十六中九年级上学期期末数学试卷
试卷更新日期:2017-01-03 类型:期末考试
一、仔细选一选
-
1. 抛物线y=(x﹣2)2+3的对称轴是( )A、直线x=2 B、直线x=3 C、直线x=﹣2 D、直线x=﹣32. 两个相似多边形的面积之比是1:4,则这两个相似多边形的周长之比是( )A、1:2 B、1:4 C、1:8 D、1:163. 如图,⊙O的半径为5,弦心距OC=3,则弦AB的长是( )
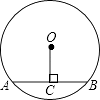 A、4 B、6 C、8 D、54. 如图,在△ABC中,DE∥BC,若 ,DE=4,则BC=( )
A、4 B、6 C、8 D、54. 如图,在△ABC中,DE∥BC,若 ,DE=4,则BC=( )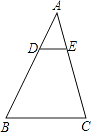 A、9 B、10 C、11 D、125. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )
A、9 B、10 C、11 D、125. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F,已知AB=2,AC=5,DF=6,则DE的长是( )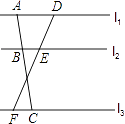 A、3 B、 C、 D、6. 分别把下列图形围起来得到的立体图形是圆锥的是( )
A、3 B、 C、 D、6. 分别把下列图形围起来得到的立体图形是圆锥的是( )
A、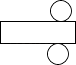 B、
B、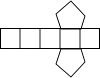 C、
C、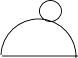 D、
D、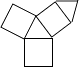 7. 如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
7. 如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )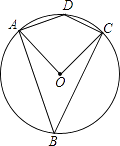 A、80° B、100° C、60° D、40°8. 在同一坐标平面内,图象不可能由函数y=2x2+1的图象通过平移变换、轴对称变换得到的函数是( )A、y=2(x+1)2﹣1 B、y=2x2+3 C、y=﹣2x2﹣1 D、y= x2﹣19. 有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y= (x>0),y=﹣ (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )A、 B、 C、 D、110. 如图,在平面直角坐标系中,A(﹣5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
A、80° B、100° C、60° D、40°8. 在同一坐标平面内,图象不可能由函数y=2x2+1的图象通过平移变换、轴对称变换得到的函数是( )A、y=2(x+1)2﹣1 B、y=2x2+3 C、y=﹣2x2﹣1 D、y= x2﹣19. 有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是y=2x,y=x2﹣3(x>0),y= (x>0),y=﹣ (x<0),将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是y随x的增大而增大的概率是( )A、 B、 C、 D、110. 如图,在平面直角坐标系中,A(﹣5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )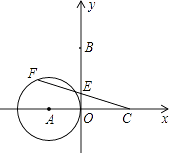 A、 B、40 C、20 D、
A、 B、40 C、20 D、二、认真填一填
-
11. 如图,某登山运动员从营地A沿坡度为1: 的斜坡AB到达山顶B,如果AB=1000米,则他实际上升了米.
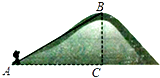 12. 如图,抛物线y1=﹣x2+4x和直线y2=2x在同一直角坐标系中.当y1>y2时,x的取值范围是 .
12. 如图,抛物线y1=﹣x2+4x和直线y2=2x在同一直角坐标系中.当y1>y2时,x的取值范围是 .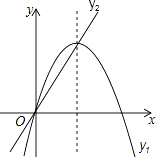 13. 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.
13. 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.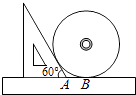 14. 已知 = ,那么 = .15. 如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第块.
14. 已知 = ,那么 = .15. 如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第块.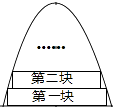 16. 如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角).
16. 如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角).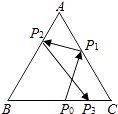 (1)、若∠P2P3B=45°,CP1=;(2)、若 <BP3< ,则P1C长的取值范围是 .
(1)、若∠P2P3B=45°,CP1=;(2)、若 <BP3< ,则P1C长的取值范围是 .三、全面解一解
-
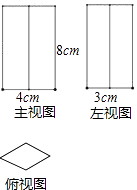
17. 计算:(﹣ )﹣1+ tan30°﹣sin245°+(2016﹣cos60°)0 .18. 一个直四棱柱的三视图如图所示,俯视图是一个菱形,求这个直四棱柱的表面积.
 19. 如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
19. 如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)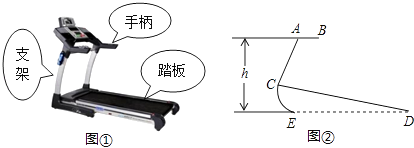 20. 将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形, 与直径AB交于点C,连接点C与圆心O′.
20. 将两张半径均为10的半圆形的纸片完全重合叠放一起,上面这张纸片绕着直径的一端B顺时针旋转30°后得到如图所示的图形, 与直径AB交于点C,连接点C与圆心O′.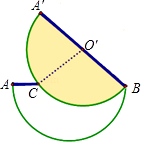 (1)、求 的长;(2)、求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白 .21. 如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.
(1)、求 的长;(2)、求图中下面这张半圆形纸片未被上面这张纸片重叠部分的面积S白 .21. 如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E.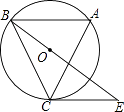 (1)、求∠BCE的度数;(2)、若⊙O半径为3,求BE长.22.
(1)、求∠BCE的度数;(2)、若⊙O半径为3,求BE长.22.如图,抛物线y=﹣x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF OC,连接OE,CF得四边形OCFE.
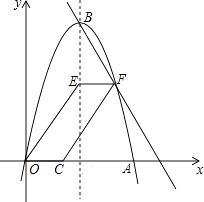 (1)、求B点坐标;(2)、当tan∠EOC= 时,显然满足条件的四边形有两个,求出相应的点F的坐标;
(1)、求B点坐标;(2)、当tan∠EOC= 时,显然满足条件的四边形有两个,求出相应的点F的坐标;
(3)、当0<tan∠EOC<3时,对于每一个确定的tan∠EOC值,满足条件的四边形OCFE有两个,当这两个四边形的面积之比为1:2时,求tan∠EOC.23.要利用28米长的篱笆和一堵最大可利用长为12米的墙围成一个如图1的一边靠墙的矩形养鸡场,在围建的过程中遇到了以下问题,请你帮忙来解决.
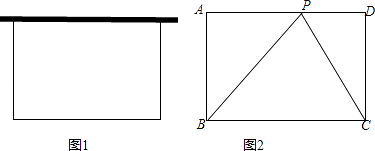 (1)、这个矩形养鸡场要怎样建面积能最大?求出这个矩形的长与宽;(2)、在(1)的前提条件下,要在墙上选一个点P,用不可伸缩的绳子分别连接BP,CP,点P取在何处所用绳子长最短?(3)、仍然是矩形养鸡场面积最大的情况下,若把(2)中的不可伸缩的绳子改为可以伸缩且有弹性的绳子,点P可以在墙上自由滑动,求sin∠BPC的最大值.24.
(1)、这个矩形养鸡场要怎样建面积能最大?求出这个矩形的长与宽;(2)、在(1)的前提条件下,要在墙上选一个点P,用不可伸缩的绳子分别连接BP,CP,点P取在何处所用绳子长最短?(3)、仍然是矩形养鸡场面积最大的情况下,若把(2)中的不可伸缩的绳子改为可以伸缩且有弹性的绳子,点P可以在墙上自由滑动,求sin∠BPC的最大值.24.如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y= x2﹣2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=﹣6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.
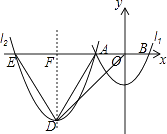 (1)、求抛物线l2的解析式;(2)、求证:△ADE∽△DOE;(3)、半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F(﹣6,0),运动速度为1单位/秒,运动时间为t秒,⊙P绕着点C顺时针旋转90°得⊙P1 , 随着⊙P的运动,求P1的运动路径长以及当⊙P1与y轴相切的时候t的值.
(1)、求抛物线l2的解析式;(2)、求证:△ADE∽△DOE;(3)、半径为1的⊙P的圆心P沿着直线x=﹣6从点D运动到F(﹣6,0),运动速度为1单位/秒,运动时间为t秒,⊙P绕着点C顺时针旋转90°得⊙P1 , 随着⊙P的运动,求P1的运动路径长以及当⊙P1与y轴相切的时候t的值.