2015-2016学年浙江省嘉兴市九年级上学期期末数学试卷

试卷更新日期：2017-01-03 类型：期末考试

进入出卷网下载

一、选择题

1. 下列函数属于二次函数的是（）

A、y=2x﹣1 B、y= $\frac{1}{x^{2}} + 3$ C、y=x²+2x﹣3 D、y= $\frac{5}{x}$

查看试题解析
2. 下列事件中，不可能事件是（）

A、今年的除夕夜会下雪 B、在只装有红球的袋子里摸出一个黑球 C、射击运动员射击一次，命中10环 D、任意掷一枚硬币，正面朝上

查看试题解析
3. 若 $\frac{a}{b} = \frac{3}{5}$ ，则 $\frac{a + b}{b}$ 的值为（）

A、 $\frac{8}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{2}$ D、 $\frac{5}{8}$

查看试题解析
4. 下列命题正确的是（）

A、三点确定一个圆 B、平分弦的直径垂直于弦 C、等圆中相等的圆心角所对的弧相等 D、圆周角的度数等于圆心角度数的一半

查看试题解析
5. 如图，l₁∥l₂∥l₃ ，直线a，b与l₁、l₂、l₃分别相交于A，B，C和点D，E，F．若 $\frac{A B}{B C}$ = $\frac{2}{3}$ ，DE=4，则EF的长是（）

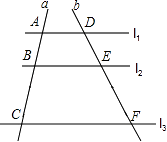A、 $\frac{8}{3}$ B、 $\frac{20}{3}$ C、6 D、10

查看试题解析
6. 对于抛物线y=﹣2（x﹣1）²+3，下列判断正确的是（）

A、抛物线的开口向上 B、抛物线的顶点坐标是（﹣1.3） C、当x=3时，y＞0 D、方程﹣2（x﹣1）²+3=0的正根在2与3之间

查看试题解析
7. 如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，若⊙O的直径为4，则弦AB长为（）

A、2 B、3 C、 $\sqrt{2}$ D、 $\sqrt{3}$

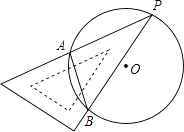查看试题解析
8. 对一批衬衣进行抽检，统计合格衬衣的件数，得到如下的频数表：
抽查件数（件）
100
150
200
500
800
1000
合格频数
85
141
176
445
724
900
根据表中数据，下列说法错误的是（）

A、抽取100件的合格频数是85 B、任抽取一件衬衣是合格品的概率是0.8 C、抽取200件的合格频率是0.88 D、出售1200件衬衣，次品大约有120件

查看试题解析
9. 如图，点G是△ABC的重心，下列结论：① $\frac{D G}{G B} = \frac{1}{2}$ ；② $\frac{A E}{E B} = \frac{E D}{B C}$ ；③△EDG∽△CGB；④ $\frac{S_{四边形 A E G D}}{S_{△ A B C}} = \frac{1}{3}$ ．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在△ABC中，∠A=40°，BC=3，分别以点B，C为圆心，BC长为半径在BC右侧画弧，两弧交于点D，与AB，AC的延长线分别交于点E，F，则弧DE和弧DF的长度和为（）

A、 $\frac{3 π}{2}$ B、 $\frac{5 π}{3}$ C、 $\frac{7 π}{3}$ D、2π

查看试题解析

二、填空题

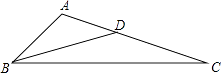
11. 正六边形的每个内角的度数是度．

查看试题解析
12. 将抛物线y=x²向左平移1个单位后的抛物线表达式为．

查看试题解析
13. 如图，点D在△ABC的边AC上，若要使△ABD与△ACB相似，可添加的一个条件是（只需写出一个）．

查看试题解析
14. 有8张形状、大小均相同的卡片，每张卡片的背面分别写有不同的从1到8的一个自然数，从中任意抽出一张，卡片上的数是3的倍数的概率是．

查看试题解析
15. 如图，矩形ABCD的顶点A、C分别在x轴、y轴上，点B在第一象限，若函数y=ax²﹣2ax+1的图象经过点B、C，则点B的坐标是

查看试题解析
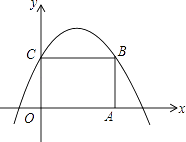16. 如图，水平放置的圆柱形排水管的截面半径为10cm，截面中有水部分弓形高为5cm，则水面宽AB为 cm．

查看试题解析
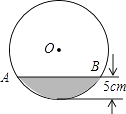17. 如图，用长为24m的篱笆，一面利用墙（墙足够长）围成一块留有一扇tm宽门的长方形花圃．设花圃宽AB为xm，面积为ym² ，则y与x的函数表达式为

查看试题解析
18. 如图，已知⊙O的半径为5，弦AB=8，点E在AB上运动，连结OE，过点E作EF⊥OE交⊙O于点F，当EF最大时，OE+EF的值为

查看试题解析
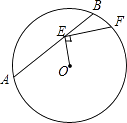19. 如图，已知矩形ABCD∽矩形BCFE，AD=AE=1，则AB的长为

查看试题解析
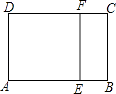20. 如图，半圆O的直径AC=2 $\sqrt{2}$ ，点B为半圆的中点，点D在弦AB上，连结CD，作BF⊥CD于点E，交AC于点F，连结DF，当△BCE和△DEF相似时，BD的长为．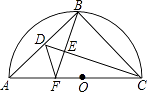

查看试题解析

三、解答题

21. 已知二次函数y=x²+2x+m的图象过点A（3，0）．

(1)、求m的值；

(2)、当x取何值时，函数值y随x的增大而增大．

查看试题解析
22. 如图，在边长为1的正方形组成的网格中，点A、B、C都在格点上，将△ABC绕点A按逆时针方向旋转90°，得到△AB′C′．

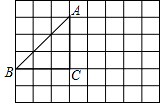(1)、画出旋转后的△AB′C′；

(2)、求边AB在旋转过程中扫过的面积．

查看试题解析
23. 一个布袋里装有红色、黄色、黑色三个球，它们除颜色外其余都相同，从中任意摸出1个球，记下颜色后放回，搅匀，再摸出1个球．

(1)、请用树状图或列表法列举出两次摸球可能出现的各种结果；

(2)、摸到的两个球颜色相同的概率是多少？

查看试题解析
24. 如图，已知在Rt△ABC与Rt△ECD中，∠ACB=∠ECD=90°，CD为Rt△ABC斜边上的中线，且ED∥BC．

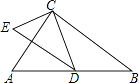(1)、求证：△ABC∽△EDC；

(2)、若CE=3，CD=4，求CB的长．

查看试题解析
25. 某水果大卖场每日批量进货销售某种水果，假设日销售量与日进货量相等．设该水果进货量为x千克，每千克进货成本为y元，每千克售价为s元，y与x的关系如图，s与x满足关系式：s=﹣ $\frac{1}{15}$ x+12．

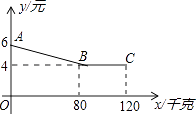(1)、请解释图中线段BC的实际意义；

(2)、该水果进货量为多少时，获得的日销售利润最大？最大利润是多少？

查看试题解析
26. 如图，已知抛物线y=﹣x²+3x与x轴的正半轴交于点A，点B在抛物线上，且横坐标为2，作BC⊥x轴于点C，⊙B经过原点O，点E为⊙B上一动点，点F在AE上．

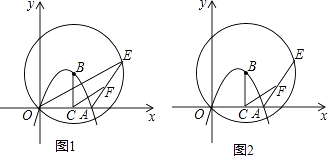(1)、求点A的坐标；

(2)、如图1，连结OE，当AF：FE=1：2时，求证：△ACF∽△AOE；

(3)、如图2，当点F是AE的中点时，求CF的最大值．

查看试题解析

抽查件数（件）	100	150	200	500	800	1000
合格频数	85	141	176	445	724	900