2015-2016学年浙江省杭州市上城区八年级上学期期末数学试卷
试卷更新日期:2017-01-03 类型:期末考试
一、仔细选一选
-
1. 已知三角形的两边长分别为8和4,则第三边长可能是( )A、3 B、4 C、8 D、122. 平面直角坐标系内有一点A(a,﹣a),若a>0,则点A位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若m>n,则下列不等式成立的是( )A、﹣3m>﹣2n B、am>an C、a2m>a2n D、m﹣3>n﹣34. 在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )A、C,r B、C,π,r C、C,πr D、C,2π,r5. 如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的( )
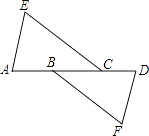 A、AB=CD B、EC=BF C、∠A=∠D D、AB=BC6. 在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )A、3 B、3.6 C、4 D、4.87. 等腰三角形的一个内角为70°,它的一腰上的高与底边所夹的角的度数是( )A、35° B、20° C、35°或20° D、无法确定8. 如图,直线y=﹣x+m与y=nx+4n的交点的横坐标为﹣2,则关于x的不等式nx+4n>﹣x+m>0的整数解可能是( )
A、AB=CD B、EC=BF C、∠A=∠D D、AB=BC6. 在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,则BC边上的高线长是( )A、3 B、3.6 C、4 D、4.87. 等腰三角形的一个内角为70°,它的一腰上的高与底边所夹的角的度数是( )A、35° B、20° C、35°或20° D、无法确定8. 如图,直线y=﹣x+m与y=nx+4n的交点的横坐标为﹣2,则关于x的不等式nx+4n>﹣x+m>0的整数解可能是( ) A、1 B、﹣1 C、﹣2 D、﹣39. 如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1 , 再过点A1作x轴的垂线交直线于点B1 , 以点A为圆心,AB1长为半径画弧交x轴于点A2 , …,按此做法进行下去,则点B4的坐标是( )
A、1 B、﹣1 C、﹣2 D、﹣39. 如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1 , 再过点A1作x轴的垂线交直线于点B1 , 以点A为圆心,AB1长为半径画弧交x轴于点A2 , …,按此做法进行下去,则点B4的坐标是( ) A、(2 ,2 ) B、(3,4) C、(4,4) D、(4 ﹣1,4 )10. 在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P.Q也随之移动,若限定点P,Q分别在线段AB,AD边上移动,则点A′在BC边上可移动的最大距离为( )
A、(2 ,2 ) B、(3,4) C、(4,4) D、(4 ﹣1,4 )10. 在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P.Q也随之移动,若限定点P,Q分别在线段AB,AD边上移动,则点A′在BC边上可移动的最大距离为( )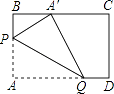 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、认真填一填
-
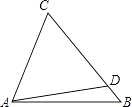
11. 命题“直角三角形两锐角互余”的逆命题是: .12. 在平面直角坐标系中,点(﹣1,2)关于y轴对称的点的坐标是 .13. 已知A(1,1)是平面直角坐标系内一点,若以y轴的正方向为正北方向,以x轴的正方向为正东方向,则点A位于坐标原点O的度方向,与点O的距离为 .14. 在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过的象限是 .15. 如图,在△ABC中,D是BC上一点,AC=CD,∠DAB=10°,则∠CAB﹣∠B= .
 16. 不等式组 的解集是x>2,则m的取值范围是 .17. 如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后分钟,甲乙两人第一次走在同一条边上.
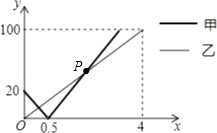
16. 不等式组 的解集是x>2,则m的取值范围是 .17. 如图,在边长为100米的正三角形花坛的边上,甲、乙两人分别从两个顶点同时出发,按逆时针方向行走,已知甲的速度是42米/分,乙的速度是34米/分.出发后分钟,甲乙两人第一次走在同一条边上.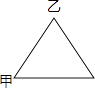 18. 沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
18. 沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:①甲船的速度是25km/h;
②从A港到C港全程为120km;
③甲船比乙船早1.5小时到达终点;
④图中P点为两者相遇的交点,P点的坐标为( );
⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是 <x<2.
其中正确的结论有 .
三、全面答一答
-
19. 解答(1)、解不等式 >1﹣ ,并把它的解集在数轴上表示出来.(2)、一个长方形足球训练场的长为xm,宽为70m.如果它的周长大于350m,面积小于7560m2 , 请确定x的取值范围.20. 如图,在Rt△ABC中,∠ACB=90°.
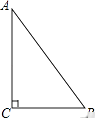 (1)、实践与操作:利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法);
(1)、实践与操作:利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法);①作AB的垂直平分线交AB于点D,连接CD;
②分别作∠ADC、∠BDC的平分线,交AC、BC于点E、F.
(2)、求证:CE=DF.21. 强强和佳佳一起去旅游,在某个景点分别乘两个热气球观光.强强坐1号热气球从海拔60m处出发,以2m/min的速度上升.与此同时,佳佳坐2号热气球从海拔120m处出发,以1m/min的速度上升.设两个热气球上升的时间均为xmin(0≤x≤80),上升过程中达到的海拔高度分别为y1 , y2 .(1)、直接写出y1 , y2关于x的函数表达式;(2)、写出两个气球海拔高度差y0关于x的函数解析式:当30≤x≤80时,两个气球所在位置的海拔最多相差多少米?22. 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.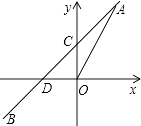 (1)、m=;(2)、若一次函数图象经过点B(﹣2,﹣1),求一次函数的解析式;(3)、在(2)的条件下,求△AOD的面积.23. 在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.
(1)、m=;(2)、若一次函数图象经过点B(﹣2,﹣1),求一次函数的解析式;(3)、在(2)的条件下,求△AOD的面积.23. 在直线上顺次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.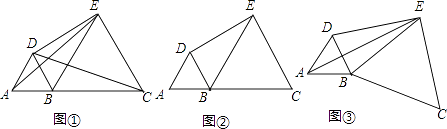 (1)、如图①,连结CD,AE,求证:CD=AE;(2)、如图②,若AB=1,BC=2,求DE的长;(3)、如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.24. A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.
(1)、如图①,连结CD,AE,求证:CD=AE;(2)、如图②,若AB=1,BC=2,求DE的长;(3)、如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有DE2+BE2=AE2 , 试求∠DEB的度数.24. A(0,4)是直角坐标系y轴上一点,P是x轴上一动点,从原点O出发,沿正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒. (1)、若AB∥x轴,求t的值;(2)、设点B的坐标为(x,y),试求y关于x的函数表达式;(3)、当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标.
(1)、若AB∥x轴,求t的值;(2)、设点B的坐标为(x,y),试求y关于x的函数表达式;(3)、当t=3时,平面直角坐标系内有一点M(3,a),请直接写出使△APM为等腰三角形的点M的坐标.