2015-2016学年浙江省杭州市经济开发区八年级上学期期末数学试卷

试卷更新日期：2017-01-03 类型：期末考试

进入出卷网下载

一、选择题

1. 下列“表情图”中，属于轴对称图形的是

A、 B、 C、 D、

查看试题解析
2. 若x＞y，则下列式子正确的是（）

A、y+1＞x﹣1 B、 $\frac{x}{3}$ ＞ $\frac{y}{3}$ C、1﹣x＞1﹣y D、﹣3x＞﹣3y

查看试题解析
3. 下列坐标系表示的点在第四象限的是（）

A、（0，﹣1） B、（1，1） C、（2，﹣1） D、（﹣1，2）

查看试题解析
4.
如图，在△ABC中，AB=AC，∠A=40°，ED为AB垂直平分线，则∠EBC的度数是（　　）

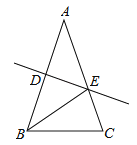A、50° B、40° C、30° D、70°

查看试题解析
5. 下列命题：
①有一条直角边和斜边对应相等的两个直角三角形全等；
②周长相等的两个三角形是全等三角形；
③全等三角形对应边上的高、中线、对应角的角平分线相等；
④两个含60°角的等腰三角形是全等三角形；
其中正确的命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 一次函数y=kx+b（k，b，k≠0）的图象如图所示，当y＜0时，自变量x的取值范围是（）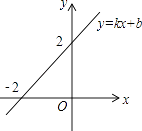

A、x＜﹣2 B、x＞﹣2 C、x＞2 D、x＜2

查看试题解析
7. 若正三角形的边长为2cm，则这个正三角形的面积是（）cm² ．

A、6 B、4 C、2 $\sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
8. 已知直角三角形的两边分别为6和8，则斜边上的中线长为（）

A、20 B、5 C、4 D、4或5

查看试题解析
9.
如图，在平面直角坐标系中，等腰直角三角形ABC的腰长为2，直角顶点A在直线l：y=2x+2上移动，且斜边BC∥x轴，当△ABC在直线l上移动时，BC的中点D满足的函数关系式为（）

A、y=2x B、y=2x+1 C、y=2x+2﹣ $\sqrt{2}$ D、y=2x﹣ $\sqrt{2}$

查看试题解析
10. 如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：
①∠AOB=90°+ $\frac{1}{2}$ ∠C；

②AE+BF=EF；

③当∠C=90°时，E，F分别是AC，BC的中点；

④若OD=a，CE+CF=2b，则S_△_CEF=ab．

其中正确的是（）

A、①② B、③④ C、①②④ D、①③④

查看试题解析

二、填空题

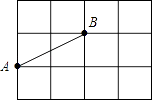
11. 已知点A（m，3）与点B（2，n）关于y轴对称，则m= ， n= ．

查看试题解析
12. “若a＞0，b＞0，则ab＞0”的逆命题是，该逆命题是一个命题（填“真”或“假”）

查看试题解析
13. 已知关于x的一元一次方程4x+m﹣1=3m+1的解是负数，则m的取值范围是．

查看试题解析
14. 如图，是由边长为1个单位长度的小正方形的网格，在格点中找一点C，使△ABC是等腰三角形，这样的点C有个．

查看试题解析
15. 在直角坐标系中，正方形A₁B₁C₁O₁、A₂B₂C₂C₁、…、A_nB_nC_nC_n_﹣₁按如图所示的方式放置，其中点A₁、A₂、A₃、…、A_n均在一次函数y=kx+b的图象上，点C₁、C₂、C₃、…、C_n均在x轴上．若点B₁的坐标为（1，1），点B₂的坐标为（3，2），则点A_n的坐标为．

查看试题解析
16. 有一块直角三角形绿地，量得两直角边长分别为3m，4m，现在要将绿地扩充成等腰三角形，且扩充时只能延长两条直角边中的一条，则扩充后等腰三角形绿地的面积为m² ．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{matrix} x - 4 \geq 3 (x - 2) \\ \frac{7 x + 11}{3} - 1 > - x \end{matrix}$ ，并把它的解集在数轴上表示出来．

查看试题解析
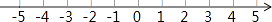18. “综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．

(1)、用记号（a，b，c）（a≤b≤c）表示一个满足条件的三角形，如（2，3，3）表示边长分别为2，3，3个单位长度的一个三角形．请列举出所有满足条件的三角形．

(2)、用直尺和圆规作出三边满足a＜b＜c的三角形（用给定的单位长度，不写作法，保留作图痕迹）．
$\frac{1}{单位长度}$

查看试题解析
19. 下面是小刚解的一道题：
题目：如图，AB=AD，∠B=∠D，说明：BC=DC．
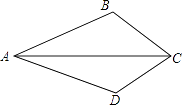
解：在△ABC和△ADC中，
${\begin{matrix} A B = A D \\ ∠ B = ∠ D \\ A C = A C \end{matrix}$
∴△ABC≌△ADC，∴BC=DC
你认为小刚解法正确吗？若正确，说明理由；若不正确，请将小刚做的错误指出，并给出你认为正确的解法．

查看试题解析
20. 某西瓜产地组织40辆汽车装运A、B、C三种西瓜共200吨到外地销售，按计划，40辆汽车都要装运，每辆汽车只能装运同一种西瓜，且必须装满．根据下表提供的信息，解答以下问题：
西瓜种类
A
B
C
每辆汽车运载量（吨）
4
5
6
每吨西瓜获利（百元）
16
10
12

(1)、设装运A种西瓜的车数为x，装运B种西瓜的车数为y，求y与x的函数关系式；

(2)、如果装运每种西瓜的车辆数都不少于12辆，那么车辆的安排方案有几种？哪一种方案获利最多，最多利润是多少？

查看试题解析
21. 如图，已知函数y=x+1的图象与y轴交于点A，一次函数y=4x+a的图象与x轴以及y=x+1的图象分别交于点C，B．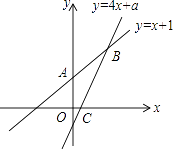

(1)、若点B的横坐标为1，求四边形AOCB的面积；

(2)、若一次函数y=4x+a的图象与函数y=x+1的图象的交点B始终在第一象限，求a的取值范围．

查看试题解析
22. 学完第2章“特殊的三角形”后，老师布置了一道思考题：
如图，点M、N分别在正三角形ABC的BC，CA边上，且BM=CN，AM，BN交于点Q．

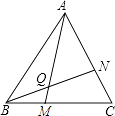(1)、判断△ABM与△BCN是否全等，并说明理由．

(2)、判断∠BQM是否会等于60°，并说明理由．

(3)、若将题中的点M，N分别移动到BC，CA的延长线上，且BM=CN，是否能得到∠BQM=60°？请说明理由．

查看试题解析
23. 某校部分住校生放学后到学校开水房打水，每人接水2升，他们先同时打开两个放水龙头，后来因故障关闭一个放水龙头，假设前后两人接水间隔时间忽略不计，且不发生泼洒，锅炉内的余水量m（升）与接水时间t（分）的函数关系图象如图所示，请结合图象，回答下列问题：

(1)、请直接写出m与t之间的函数关系式：．

(2)、前15位同学接水结束共需要几分钟？

(3)、小敏说“今天我们寝室的8位同学去开水房连续接完水恰好用了3分钟．”你说可能吗？请说明理由．

查看试题解析

西瓜种类	A	B	C
每辆汽车运载量（吨）	4	5	6
每吨西瓜获利（百元）	16	10	12