2018年浙江省金华市中考数学冲刺模拟卷（2）

试卷更新日期：2018-06-01 类型：中考模拟

进入出卷网下载

一、选择题

1. 如果|a|=a，下列各式成立的是（）

A、a＞0 B、a＜0 C、a≥0 D、a≤0

查看试题解析
2. 如图是某几何体的三视图，则该几何体的全面积等于（）

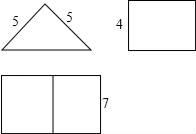A、112 B、136 C、124 D、84

查看试题解析
3. 边长为a的等边三角形，记为第1个等边三角形，取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形，取这个正六边形不相邻的三边中点，顺次连接又得到一个等边三角形，记为第2个等边三角形，取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图），…，按此方式依次操作，则第6个正六边形的边长为（）

A、 $\frac{1}{3} \times {(\frac{1}{2})}^{5} a$ B、 $\frac{1}{2} \times {(\frac{1}{3})}^{5} a$ C、 $\frac{1}{3} \times {(\frac{1}{2})}^{6} a$ D、 $\frac{1}{2} \times {(\frac{1}{3})}^{6} a$

查看试题解析
4. 已知点A，B分别在反比例函数y= $\frac{2}{x}$ （x＞0），y= $\frac{- 8}{x}$ （x＞0）的图象上且OA⊥OB，则tanB为（）

A、 $\frac{1}{\sqrt{2}}$ B、 $\frac{1}{2}$ C、 $\frac{1}{\sqrt{3}}$ D、 $\frac{1}{3}$

查看试题解析
5. 下列各式中，相等关系一定成立的是（　　）

A、（x﹣y）²=（y﹣x）² B、（x+6）（x﹣6）=x²﹣6 C、（x+y）=x²+y² D、（3x﹣y）（﹣3x+y）=9x²﹣y²

查看试题解析
6. 抛物线y=ax²+bx+3（a≠0）过A（4，4），B（2，m）两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是（）

A、m≤2或m≥3 B、m≤3或m≥4 C、2＜m＜3 D、3＜m＜4

查看试题解析
7.
如图，用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为（　　）

A、 $\frac{2 - \sqrt{2}}{4} a$ B、 $\frac{\sqrt{2} - 1}{2} a$ C、 $(\sqrt{2} - 1) a$ D、 $(2 - \sqrt{2}) a$

查看试题解析
8. 某校组织九年级学生参加中考体育测试，共租3辆客车，分别编号为1、2、3，李军和赵娟两人可任选一辆车乘坐，则两人同坐2号车的概率为（　　）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
9. 不等式组 ${\begin{matrix} x + 5 < 5 x + 1 \\ x - m > 1 \end{matrix}$ 的解集是x＞1，则m的取值范围是（）

A、m≥1 B、m≤1 C、m≥0 D、m≤0

查看试题解析
10.
某学校为了提升学生素质，要求学生利用休息时间参加社会实践活动．四月的一个星期天，该校学生小慧去市美术馆参观“中国梦•精品中国画”美术作品展．据展览说明介绍，参观作品时人眼看作品的视角α是30°时欣赏美术作品的效果最佳．当小慧看到一幅2米×2米的作品时（如图所示）发现该作品挂在墙面上的顶端A点距离地面3.8米．若小慧的眼睛距离地面1.60米，当看到该作品的效果达到最佳时，小慧的眼睛距离挂美术作品的墙面的最远距离是（　　）

A、4米 B、2 $\sqrt{3}$ 米 C、（2+ $\sqrt{3}$ ）米 D、（ $\sqrt{3}$ +1.6）米

查看试题解析

二、填空题

11. 因式分解：9x²﹣4= ．

查看试题解析
12. 已知m²－5m－1＝0，则2m²－5m＋ $\frac{1}{m^{2}}$ ＝

查看试题解析
13. 一组数据2，x，4，3，3的平均数是3，则这组数据的中位数是．

查看试题解析
14. 如图，a∥b，直线a，b被直线c所截，AC₁ ， BC₁分别平分∠EAB，∠FBA，AC₂ ， BC₂分别平分∠EAC₁ ， ∠FBC₁；AC₃ ， BC₃分别平分∠EAC₂ ， ∠FBC₂交于点C₃…依次规律，得点C_n ，则∠C₃=度，∠C_n=度．

查看试题解析
15. 如图，四边形OABC是平行四边形，点C在x轴上，反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为．

查看试题解析
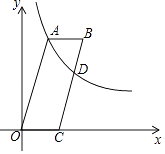16.
如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B，有人在直线AB上点C（靠点B一侧）竖直向上摆放若干个无盖的圆柱形桶．试图让网球落入桶内，已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．当竖直摆放圆柱形桶至少个时，网球可以落入桶内．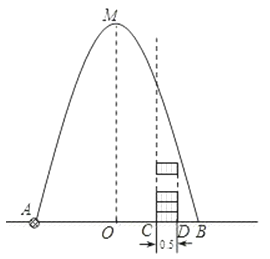

查看试题解析

三、解答题

17. 计算：（2 $\sqrt{2}$ ﹣π）⁰﹣4cos60°+| $\sqrt{2}$ ﹣2|﹣ $\sqrt{18}$ ．

查看试题解析
18. 如果k是数据2，5，3，8，8中的中位数，求关于x的方程 $\frac{1 - x}{2 x - 1}$ + $\frac{k}{1 - 2 x}$ =1的解．

查看试题解析
19. 如图，在正方形网格中， $△ A B C$ 的三个顶点都在格点上，点 $A 、 B 、 C$ 的坐标分别为 $(- 2 ， 4)$ 、 $(- 2 ， 0)$ 、 $(- 4 ， 1)$ ，试解答下列问题：

(1)、①画出 $△ A B C$ 关于原点 $O$ 对称的 $△ A_{1} B_{1} C_{1}$ ；②平移 $△ A B C$ ，使点 $A$ 移到点 $A_{2} (0 ， 2)$ ，画出平移后的 $△ A_{2} B_{2} C_{2}$ 并写出点 $B_{2}$ 、 $C_{2}$ 的坐标；

(2)、在 $△ A B C$ 、 $△ A_{1} B_{1} C_{1}$ 、 $△ A_{2} B_{2} C_{2}$ 中， $△ A_{2} B_{2} C_{2}$ 与哪个图形成中心对称？试写出其对称中心的坐标．

查看试题解析
20. 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如下统计图表：
学生最喜爱的节目人数统计表
节目
人数（名）
百分比
最强大脑
5
10%
朗读者
15
b%
中国诗词大会
a
40%
出彩中国人
10
20%
根据以上提供的信息，解答下列问题：

(1)、x= ， a= ， b=；

(2)、补全上面的条形统计图；

(3)、若该校共有学生1000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名．

查看试题解析
21. 经市场调查，某种商品在第x天的售价与销量的相关信息如下表；已知该商品的进价为每件30元，设销售该商品每天的利润为y元．
时间x（天）
1≤x≤50
50≤x≤90
售价（元/件）
x+40
90
每天销量（件）
200-2x

(1)、求出y与x的函数关系式

(2)、问销售该商品第几天时，当天销售利润最大？最大利润是多少？

(3)、该商品销售过程中，共有多少天日销售利润不低于4800元？直接写出答案．

查看试题解析
22.
如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，线段CD=10，连接BD；
（1）求证：∠CDE=∠DOC=2∠B；
（2）若BD：AB= $\sqrt{3}$ ：2，求⊙O的半径及DF的长．

查看试题解析
23.
如图，△ABC是等腰直角三角形，∠ACB=90°，AB=4cm，动点P以1cm/s的速度分别从点A、B同时出发，点P沿A→B向终点B运动，点Q沿B→A向终点A运动，过点P作PD⊥AC于点D，以PD为边向右侧作正方形PDEF，过点Q作QG⊥AB，交折线BC﹣CA于点G与点C不重合，以QG为边作等腰直角△QGH，且点G为直角顶点，点C、H始终在QG的同侧，设正方形PDEF与△QGH重叠部分图形的面积为S（cm²），点P运动的时间为t（s）（0＜t＜4）．

(1)、当点F在边QH上时，求t的值；

(2)、当正方形PDEF与△QGH重叠部分图形是四边形时，求S与t之间的函数关系式；

(3)、当FH所在的直线平行或垂直于AB时，直接写出t的值．

查看试题解析
24.
如图， $A M$ 是 $Δ A B C$ 的中线， $D$ 是线段 $A M$ 上一点（不与点 $A$ 重合）． $D E / / A B$ 交 $A C$ 于点 $F$ ， $C E / / A M$ ，连结 $A E$ ．

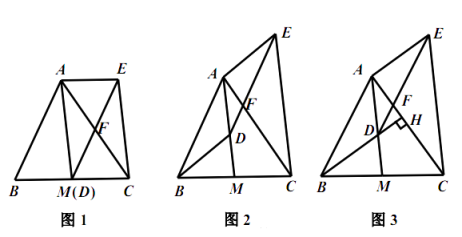(1)、如图1，当点 $D$ 与 $M$ 重合时，求证：四边形 $A B D E$ 是平行四边形；

(2)、如图2，当点 $D$ 不与 $M$ 重合时，（1）中的结论还成立吗？请说明理由.

(3)、如图3，延长 $B D$ 交 $A C$ 于点 $H$ ，若 $B H ⊥ A C$ ，且 $B H = A M$ ．当 $F H = \sqrt{3}$ ， $D M = 4$ 时，求 $D H$ 的长．

查看试题解析

节目	人数（名）	百分比
最强大脑	5	10%
朗读者	15	b%
中国诗词大会	a	40%
出彩中国人	10	20%

时间x（天）	1≤x≤50	50≤x≤90
售价（元/件）	x+40	90
每天销量（件）	200-2x