2018年浙江省嘉兴市中考数学冲刺模拟卷(2)
试卷更新日期:2018-06-01 类型:中考模拟
一、选择题
-
1. ﹣ 的相反数是( )A、 B、﹣ C、5 D、﹣52. 我国推行“一带一路”政策以来,已确定沿线有65个国家加入,共涉及总人口约达46亿人,用科学记数法表示该总人口为( )A、4.6×109 B、46×108 C、0.46×1010 D、4.6×10103. 如图所示的几何体的主视图是( )
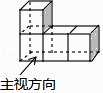 A、
A、 B、
B、 C、
C、 D、
D、 4. 分别写有数字0,﹣1,﹣2,1,3的五张卡片,除数字不同外其他均相同,从中任抽一张,那么抽到负数的概率是( )A、 B、 C、 D、5. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:①该班B等及B等以上占全班60% ②D等有4人,没有得满分的(按120分制) ③成绩分数(按120分制)的中位数在第三组 ④成绩分数(按120分制)的众数在第三组,其中正确的是( )
4. 分别写有数字0,﹣1,﹣2,1,3的五张卡片,除数字不同外其他均相同,从中任抽一张,那么抽到负数的概率是( )A、 B、 C、 D、5. 为了分析某班在四月调考中的数学成绩,对该班所有学生的成绩分数换算成等级统计结果如图所示,下列说法:①该班B等及B等以上占全班60% ②D等有4人,没有得满分的(按120分制) ③成绩分数(按120分制)的中位数在第三组 ④成绩分数(按120分制)的众数在第三组,其中正确的是( )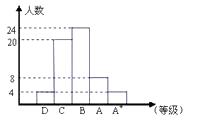 A、①② B、③④ C、①③ D、①③④6. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
A、①② B、③④ C、①③ D、①③④6. “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )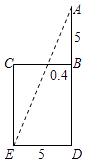 A、1.25尺 B、57.5尺 C、6.25尺 D、56.5尺7. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A、1.25尺 B、57.5尺 C、6.25尺 D、56.5尺7. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( ) A、
A、 B、
B、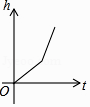 C、
C、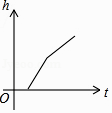 D、
D、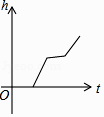 8. 下列命题中,假命题是( )A、矩形的对角线相等 B、有两个角相等的梯形是等腰梯形 C、对角线互相垂直的矩形是正方形 D、菱形的面积等于两条对角线乘积的一半9. 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是( )
8. 下列命题中,假命题是( )A、矩形的对角线相等 B、有两个角相等的梯形是等腰梯形 C、对角线互相垂直的矩形是正方形 D、菱形的面积等于两条对角线乘积的一半9. 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是( ) A、②④ B、①③ C、②③ D、①④10. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
A、②④ B、①③ C、②③ D、①④10. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )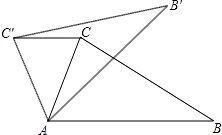 A、30° B、35° C、40° D、50°
A、30° B、35° C、40° D、50°二、填空题
-
11. 分解因式:2x3﹣2xy2= .12. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm.
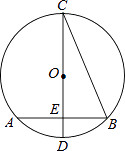 13. 如图,点P是反比例函数 (x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为 .
13. 如图,点P是反比例函数 (x<0)图象的一点,PA垂直于y轴,垂足为点A,PB垂直于x轴,垂足为点B.若矩形PBOA的面积为6,则k的值为 .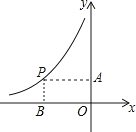 14. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
14. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .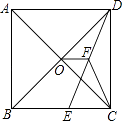 15. 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ,那么当点P运动一周时,点Q运动的总路程为 .
15. 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ,那么当点P运动一周时,点Q运动的总路程为 .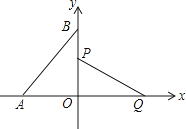 16. 如图,在△ABC中,AB=AC=2 ,∠BAC=120°,点D,E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为 .
16. 如图,在△ABC中,AB=AC=2 ,∠BAC=120°,点D,E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为 .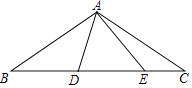
三、解答题
-
17. 计算:|﹣2|﹣2cos60°+( )﹣1﹣(π﹣ )0 .18. 某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
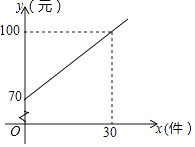 (1)、求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;(2)、已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
(1)、求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;(2)、已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
19.在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
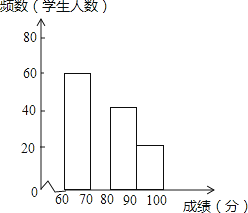 (1)、在表中的频数分布表中,m= , n= .
(1)、在表中的频数分布表中,m= , n= .成绩
频数
频率
60≤x<70
60
0.30
70≤x<80
m
0.40
80≤x<90
40
n
90≤x≤100
20
0.10
(2)、请补全图中的频数分布直方图.(3)、按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?20. 如图,建设“幸福西宁”,打造“绿色发展样板城市”.美丽的湟水河宛如一条玉带穿城而过,已形成“水清、流畅、岸绿、景美”的生态环境新格局.在数学课外实践活动中,小亮在海湖新区自行车绿道北段AC上的A,B两点分别对南岸的体育中心D进行测量,分别测得∠DAC=30°,∠DBC=60°,AB=200米,求体育中心D到湟水河北岸AC的距离约为多少米(精确到1米, ≈1.732)? 21. 某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
21. 某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)、求y与x的关系式.(2)、当x取何值时,y的值最大?(3)、如果公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?22. 在正方形 中, ,点 在边 上, ,点 是在射线 上的一个动点,过点 作 的平行线交射线 于点 ,点 在射线 上,使 始终与直线 垂直.(1)、如图1,当点 与点 重合时,求 的长;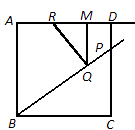 (2)、如图2,试探索: 的比值是否随点 的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(2)、如图2,试探索: 的比值是否随点 的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;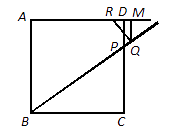 (3)、如图3,若点 在线段 上,设 , ,求 关于 的函数关系式,并写出它的定义域.
(3)、如图3,若点 在线段 上,设 , ,求 关于 的函数关系式,并写出它的定义域.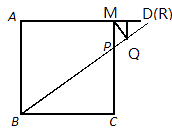 23. 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
23. 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.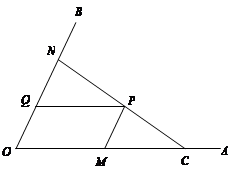 (1)、若∠AOB=60º,OM=4,OQ=1,求证:CN⊥OB.(2)、当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
(1)、若∠AOB=60º,OM=4,OQ=1,求证:CN⊥OB.(2)、当点N在边OB上运动时,四边形OMPQ始终保持为菱形.①问: 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求 的取值范围.
24. 如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x﹣15|+ =0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=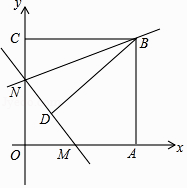 (1)、求点B的坐标;(2)、求直线BN的解析式;(3)、将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
(1)、求点B的坐标;(2)、求直线BN的解析式;(3)、将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.