湖北省广水市四中2018届数学中考模拟试卷(一)
试卷更新日期:2018-06-01 类型:中考模拟
一、单选题
-
1. |﹣2|的值是( )
A、﹣2 B、2 C、 D、﹣2. 下列计算正确的是( )A、(a+2)(a﹣2)=a2﹣2 B、(a+1)(a﹣2)=a2+a﹣2 C、(a+b)2=a2+b2 D、(a﹣b)2=a2﹣2ab+b23. 一个几何体的三视图如图所示,这个几何体是( )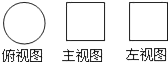 A、棱柱 B、正方形 C、圆柱 D、圆锥4. 假设五个相异正整数的平均数是15,中位数是18,则这五个相异正整数中的最大数的最大值为( )
A、棱柱 B、正方形 C、圆柱 D、圆锥4. 假设五个相异正整数的平均数是15,中位数是18,则这五个相异正整数中的最大数的最大值为( )
A、24 B、32 C、35 D、405. 下列日常现象:①用两根钉子就可以把一根木条固定在墙上;
②把弯曲的公路改直,就能够缩短路程;
③体育课上,老师测量某个同学的跳远成绩.
④建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙.
其中,可以用“两点之间,线段最短”来解释的现象正确的选项是( )
A、① B、② C、③ D、④6. 画正三角形ABC(如图)水平放置的直观图△A′B′C′,正确的是( )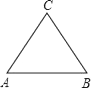 A、
A、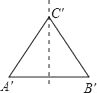 B、
B、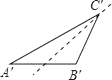 C、
C、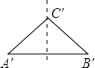 D、
D、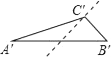 7. 一个两位数,十位上的数字x比个位上的数字y大1,若颠倒个位与十位数字的位置,得到新数比原数小9,求这个两位数列出的方程组正确的是( )
7. 一个两位数,十位上的数字x比个位上的数字y大1,若颠倒个位与十位数字的位置,得到新数比原数小9,求这个两位数列出的方程组正确的是( )
A、 B、 C、 D、8. 如图所示,图(1)中含“○”的矩形有1个,图(2)中含“○”的矩形有7个,图(3)中含“○”的矩形有17个,按此规律,图(6)中含“○”的矩形有( )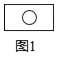
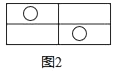
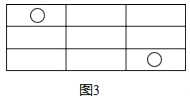 A、70 B、71 C、72 D、739. 关于二次函数y=2x2﹣mx+m﹣2,以下结论:
A、70 B、71 C、72 D、739. 关于二次函数y=2x2﹣mx+m﹣2,以下结论:①抛物线交x轴有交点;②不论m取何值,抛物线总经过点(1,0);③若m>6,抛物线交x轴于A,B两点,则AB>1;④抛物线的顶点在y=﹣2(x﹣1)2图象上.其中正确的序号是( )
A、①②③④ B、①②③ C、①②④ D、②③④10. 如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2 ,则MF的长是( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
11. 我国是世界上人均拥有淡水量较少的国家,全国淡水资源的总量约为27500亿m3 , 应节约用水,数字27500用科学记数法表示为12. 下列问题你能肯定的是(填“能”或“不能”):
(1)、钝角大于锐角:
(2)、直线比线段长:(3)、多边形的外角和都是360°:(4)、明天会下雨:
13. 如图所示,线段AB与CD都是⊙O中的弦,其中弧AB=108°,AB=a,弧CD =36°,CD=b,则⊙O的半径R=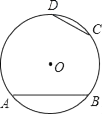 14. 点P是△ABC中AB边上的一点,过P作直线(不与AB重合)截△ABC,使截得的三角形与原三角形相似,满足条件的直线最多有条
14. 点P是△ABC中AB边上的一点,过P作直线(不与AB重合)截△ABC,使截得的三角形与原三角形相似,满足条件的直线最多有条
15. 在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, m)(m为非负数),则CA+CB的最小值是
16. 甲、乙两人从A地出发前往B地,甲先出发1分钟后,乙再出发,乙出发一段时间后返回A地取物品,甲、乙两人同时达到B地和A地,并立即掉头相向而行直至相遇,甲、乙两人之间相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则甲、乙两人最后相遇时,乙距B地的路程是米.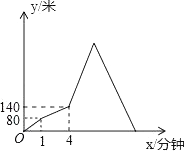
三、解答题
-
17. 计算:( )﹣2﹣(2017﹣π)0+ ﹣|﹣2|.18. 解分式方程:
(1)、 + =2(2)、 + = .19. 如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y= 的图象于点B,AB= .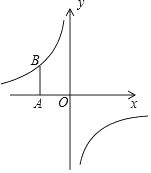 (1)、求反比例函数的解析式;(2)、若P(x1 , y1)、Q(x2 , y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2 , 指出点P、Q各位于哪个象限?并简要说明理由.
(1)、求反比例函数的解析式;(2)、若P(x1 , y1)、Q(x2 , y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2 , 指出点P、Q各位于哪个象限?并简要说明理由.
20. 如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号) 21. 某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.
21. 某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.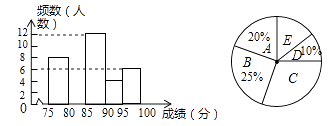
请根据图中信息,解答下列问题:
(1)、参加初赛的选手共有名,请补全频数分布直方图;
(2)、扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)、学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
22. 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.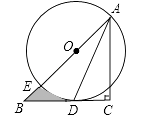 (1)、求证:AD平分∠BAC;(2)、若CD=1,求图中阴影部分的面积(结果保留π).23. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、求证:AD平分∠BAC;(2)、若CD=1,求图中阴影部分的面积(结果保留π).23. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、求出y与x的函数关系式;(2)、当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)、设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?24. 如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题: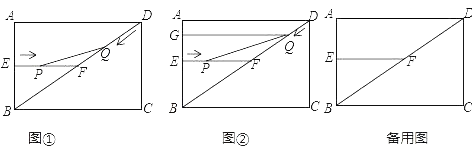 (1)、求证:△BEF∽△DCB;(2)、当点Q在线段DF上运动时,若△PQF的面积为0.6cm2 , 求t的值;(3)、如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;(4)、当t为何值时,△PQF为等腰三角形?试说明理由.25. 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣ ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)、求证:△BEF∽△DCB;(2)、当点Q在线段DF上运动时,若△PQF的面积为0.6cm2 , 求t的值;(3)、如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;(4)、当t为何值时,△PQF为等腰三角形?试说明理由.25. 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣ ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.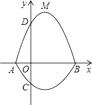 (1)、求A、B两点的坐标;(2)、“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(1)、求A、B两点的坐标;(2)、“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)、当△BDM为直角三角形时,求m的值.