黑龙江省肇源县2018届数学中考一模试卷
试卷更新日期:2018-06-01 类型:中考模拟
一、单选题
-
1. -3的绝对值等于( )A、 B、3 C、 D、2. 截止到2017年底,某市人口约为2 720 000人,将2 720 000用科学记数法表示为( )A、2.72×105 B、2.72×106 C、2.72×107 D、2.72×1083. 如图所示的几何体是由4个大小相同的小立方块搭成,它的俯视图是( )
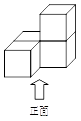 A、
A、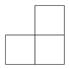 B、
B、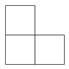 C、
C、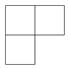 D、
D、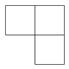 4. 下列说法正确的是( )A、对角线相等且互相垂直的四边形是菱形 B、有一个角是直角的四边形是矩形 C、对角线互相垂直的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形5. 某中学篮球队12名队员的年龄如下表:
4. 下列说法正确的是( )A、对角线相等且互相垂直的四边形是菱形 B、有一个角是直角的四边形是矩形 C、对角线互相垂直的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形5. 某中学篮球队12名队员的年龄如下表:年龄:(岁)
13
14
15
16
人数
1
5
4
2
关于这12名队员的年龄,下列说法错误的是( )
A、众数是14岁 B、极差是3岁 C、中位数是14.5岁 D、平均数是14.8岁6. 实数a,b在数轴上的位置如图所示,下列结论错误的是( )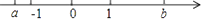 A、 < B、1<-a<b C、1< <b D、-b<a<-17. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
A、 < B、1<-a<b C、1< <b D、-b<a<-17. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、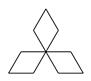 C、
C、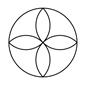 D、
D、 8. 如图,点A为反比例函数 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
8. 如图,点A为反比例函数 图象上一点,过A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )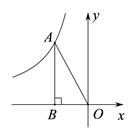 A、4 B、﹣2 C、2 D、无法确定9. 对于函数y=-2x+1,下列结论正确的是( )A、它的图象必经过点(-1,2) B、它的图象经过第一、二、三象限 C、当x>1时,y<0 D、y的值随x值的增大而增大10. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 , 边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A、4 B、﹣2 C、2 D、无法确定9. 对于函数y=-2x+1,下列结论正确的是( )A、它的图象必经过点(-1,2) B、它的图象经过第一、二、三象限 C、当x>1时,y<0 D、y的值随x值的增大而增大10. 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1 , 边B1C1与CD交于点O,则四边形AB1OD的面积是( )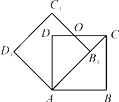 A、 B、 C、 -1 D、1+
A、 B、 C、 -1 D、1+二、填空题
-
11. 函数 的自变量x的取值范围12. sin60°的相反数是13. 一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是白球的概率为14. 分解因式: = .15. 已知二次函数y=﹣x2﹣2x+3的图象上有两点A(﹣7,y1),B(﹣8,y2),则y1y2 . (用>、<、=填空).16. 圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图的圆心角为 .17. 如图,矩形ABCD中,AD= ,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB= .
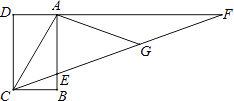 18. 下列图案是用长度相同的火柴棒按一定规律拼搭而成,第1个图案①需4根火柴棒,第2个图案②需10根火柴棒,第3个图案③需16根火柴棒,…,按此规律,第n个图案需 根火柴棒.
18. 下列图案是用长度相同的火柴棒按一定规律拼搭而成,第1个图案①需4根火柴棒,第2个图案②需10根火柴棒,第3个图案③需16根火柴棒,…,按此规律,第n个图案需 根火柴棒.
三、解答题
-
19. 计算:20. 先化简再求值: ,其中 .
21. 已知a、b是一元二次方程x2﹣2x﹣1=0的两个根且a2﹣2a﹣1=0,求a2﹣a+b+3ab的值.
22. 如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2. (1)、求一次函数的表达式;(2)、求反比例函数的表达式.23. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接DE,DG.
(1)、求一次函数的表达式;(2)、求反比例函数的表达式.23. 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接DE,DG.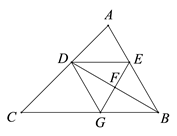 (1)、请判断四边形EBGD的形状,并说明理由;(2)、若∠ABC=60°,∠C=45°,DE= ,求BC的长.24. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
(1)、请判断四边形EBGD的形状,并说明理由;(2)、若∠ABC=60°,∠C=45°,DE= ,求BC的长.24. 某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:售价x(元/千克)
50
60
70
销售量y(千克)
100
80
60
(1)、求y与x之间的函数表达式;(2)、设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?25. 某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级(2)班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:八年级(2)班参加球类活动人数情况统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
八年级(2)班学生参加球类活动人数情况扇形统计图
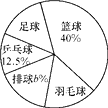
根据图中提供的信息,解答下列问题:
(1)、a= , b= .(2)、该校八年级学生共有600人,则该年级参加足球活动的人数约人;
(3)、该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
26. 某服装店用4 500元购进一批衬衫,很快售完,服装店老板又用2 100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.(1)、这两次各购进这种衬衫多少件?(2)、若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1 950元,则第二批衬衫每件至少要售多少元?
27. 如图所示,在△ABC中,AB=AC=2,∠A=90°,O为BC的中点,动点E在BA边上移动,动点F在AC边上移动.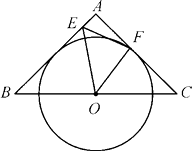 (1)、当点E,F分别为边BA,AC的中点时,求线段EF的长;(2)、当∠EOF=45°时,
(1)、当点E,F分别为边BA,AC的中点时,求线段EF的长;(2)、当∠EOF=45°时,①设BE=x,CF=y,求y与x之间的函数解析式;
②若以O为圆心的圆与AB相切(如图),试探究直线EF与⊙O的位置关系,并证明你的结论.
28. 如图,已知抛物线y= +bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的一个动点.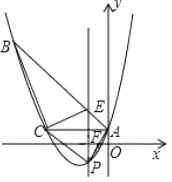 (1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP 的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP 的面积最大时,求点P的坐标;(3)、当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.