黑龙江省哈尔滨市道外区2018届数学初中升学考试模拟卷

试卷更新日期：2018-06-01 类型：中考模拟

进入出卷网下载

一、单选题

1. $\sqrt{3}$ 的相反数是（）

A、 $\sqrt{3}$ B、- $\sqrt{3}$ C、- $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 下列运算正确的是（）

A、a+a=a² B、a³÷a=a³ C、a²·a=a³ D、(a²)³=a⁵

查看试题解析
3. 下列图形是轴对称图形而不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图所示的几何体由5个大小相同的小正方体紧密摆放而成，它的左视图是（）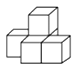

A、 B、 C、 D、

查看试题解析
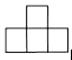5. 反比例函数 $y = \frac{m + 2}{x}$ 的图像在每一个象限内，y都随x的增大而增大．则m的取值范围是（）

A、m＜－2 B、m＞－2 C、m＞2 D、m＜2

查看试题解析
6. Rt△ACB中，∠C＝90°，AB＝5，BC=4，则tan∠A= （）

A、 $\frac{4}{3}$ B、 $\frac{4}{5}$ C、 $\frac{3}{5}$ D、 $\frac{3}{4}$

查看试题解析
7. 如图，在△ABC中，∠B=40°，将△ABC绕点A逆时针旋转至△ADE处，使点B落在BC的延长线上的D点处，则∠BDE等于（）

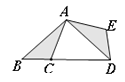A、100° B、80° C、50° D、40°

查看试题解析
8. 如图，△ABC中，DF∥BE，AD，BE相交于点G，下列结论错误的是（）

A、 $\frac{A E}{A F} = \frac{A G}{A D}$ B、 $\frac{C E}{C F} = \frac{C B}{C D}$ C、 $\frac{A E}{A F} = \frac{C F}{C E}$ D、 $\frac{G E}{D F} = \frac{A G}{A D}$

查看试题解析
9. 如图，某小区规划在一个长16m，宽9m的矩形场地ABCD上，修建同样宽的小路，使其中两条与AB平行，另一条与AD平行，其余部分种草，如果使草坪部分的总面积为112m² ，设小路的宽为xm，那么x满足的方程是（）

A、2x²-25x+16=0 B、x²-25x+32=0 C、x²-17x+16=0 D、x²-17x-16=0

查看试题解析
10. A，B两地相距90km，甲骑摩托车由A地出发，去B地办事，甲出发的同时，乙骑自行车同时由B地出发沿着同一条道路前往A地，甲办完事后原速返回A地，结果比乙早到0.5小时.甲、乙两人离A地距离y（km）与时间x（h）的函数关系图像如图所示.下列说法：①.a=3.5，b=4；② 甲走的全路程是90km；③乙的平均速度是22.5km/h；.④甲在B地办事停留了0.5小时.其中正确的说法有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 将140000用科学记数法表示为．

查看试题解析
12. 若函数y= $\frac{x}{4 x + 1}$ 有意义，则自变量x的取值范围是．

查看试题解析
13. 计算： $\sqrt{12} - 3 \sqrt{\frac{1}{3}}$ = ．

查看试题解析
14. 把多项式m³n－mn³分解因式的结果是．

查看试题解析
15. 不等式组 ${\begin{matrix} 2 x + 1 \leq 3 \\ 5 \geq 3 - x \end{matrix}$ 的解集为．

查看试题解析
16. 一个扇形的半径为3cm，面积为π cm² ，则此扇形的圆心角为度

查看试题解析
17. 一个口袋中装有2个红球、2个白球，每个球除颜色外都相同，随机从中一次摸出两球，摸到都是红球的概率是．

查看试题解析
18. 如图，已知PA、PB是⊙O的两条切线，A、B为切点．AC是⊙O 的直径，若∠P=80°，则∠BAC的度数为．

查看试题解析
19. 在正方形ABCD中，点E在直线AB上，EF⊥AC于点F，连接EC，EC=5，△EFC的周长为12，则AE的长为．

查看试题解析
20. 如图，在△ABC中，∠B=45°，在BC边上取一点D，使CD=CA，点E在AC上，连接ED，若∠AED=45°，且CE=1，BD=2，则AD的长是．

查看试题解析

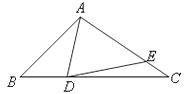
三、解答题

21. 先化简，再求代数式 $\frac{m - 1}{m} \div (2 m - \frac{1 + m^{2}}{m})$ 的值，其中m=2cos30°－tan45°

查看试题解析
22. 图1、图2分别是8×6的网格，网格中每个小正方形的边长均为1，线段AB的端点在小正方形的顶点上，请在图1、图2中各画一个图形，分别满足以下要求：

(1)、在图1中画一个以线段AB为一边周长为10+2 $\sqrt{10}$ 的平行四边形，所画图形的各顶点必须在小正方形的顶点上．

(2)、在图2中画一个以线段AB为一边的等腰三角形，所画等腰三角形的各顶点必须在小正方形的顶点上，并求出该等腰三角形的周长.

查看试题解析
23. 为了参加市举办“科学发现杯”知识竞赛活动，我区开展了预赛，400名学生参加此次比赛，为了解此次竞赛情况：
从中抽取一部分学生成绩统计如下（得分取整数，满分为100分）
分组
频数
频率
50.5-60.5
4
0.08
60.5-70.5
6

70.5-80.5
16
0.32
80.5-90.5

90.5-100.5
8
0.16
合计

1.00

(1)、补全频数分布表和频数分布直方图.

(2)、这组数据的中位数落在第几组？

(3)、若90分以上成绩为优秀，估计我区获得优秀学生约有多少？

查看试题解析
24. 如图，在△ABC中，D是BC边的中点，分别过点B、C作射线AD的垂线，垂足分别为E、F，连接BF、CE.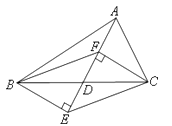

(1)、求证：四边形BECF是平行四边形；

(2)、若AF=FD，在不添加辅助线的条件下，直接写出与△ABD面积相等的所有三角形.

查看试题解析
25. 某工厂签了1200件商品订单，要求不超过15天完成.现有甲、乙两个车间来完成加工任务。已知甲车间的加工能力是乙车间加工能力的1.5倍，并且加工240件需要的时间甲车间比乙车间少用2天.

(1)、求甲、乙每个车间的加工能力每天各是多少件？

(2)、甲、乙两个车间共同生产了若干天后，甲车间接到新任务，留下乙车间单独完成剩余工作，求甲、乙两车间至少合作多少天，才能保证完成任务.

查看试题解析
26. 如图，△ABC内接于⊙O，弦AD⊥BC，垂足为H，连接OB.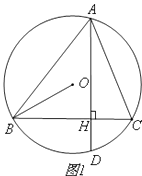

(1)、如图1，求证：∠DAC=∠ABO；

(2)、如图2，在弧AC上取点F，使∠CAF=∠BAD，在弧AB取点G，使AG∥OB，若∠BAC=60º，
求证：GF=GD；

(3)、如图3，在(2)的条件下，AF、BC的延长线相交于点E，若AF：FE=1：9，求sin∠ADG的值。

查看试题解析
27. 如图，在平面直角坐标中，抛物线y=ax²－2ax－3a(a≠0)与x轴交于A、B(A在B的左侧)，与y轴交于点C，且OC=3OA.

(1)、如图（1）求抛物线的解析式；

(2)、如图（2）动点P从点O出发，沿y轴正方向以每秒1个单位的速度移动，点D是抛物线顶点，连接PB、PD、BD，设点P运动时间为t（单位：秒），△PBD的面积为S，求S与t的函数关系式；

(3)、如图（3）在（2）的条件下，延长BP交抛物线于点Q，过点O作OE⊥BQ，垂足为E，连接CE、CB，若CE=CB，求t值，并求出此时的Q点坐标.

查看试题解析

分组	频数	频率
50.5-60.5	4	0.08
60.5-70.5	6
70.5-80.5	16	0.32
80.5-90.5
90.5-100.5	8	0.16
合计		1.00