2017-2018学年数学沪科版八年级下册第19章 四边形 单元检测
试卷更新日期:2018-06-01 类型:单元试卷
一、选择题
-
1. 如图,在▱ABCD中,AE平分∠DAB,AB=5,DE=2.则▱ABCD的周长是( )
 A、7 B、10 C、14 D、162. 如图,在▱ABCD中,AB=6,AD=9,AF平分∠BAD交BC于点E,交DC的延长线于点F,BG⊥AF于点G,BG=4 ,EF= AE,则△CEF的周长为( ).
A、7 B、10 C、14 D、162. 如图,在▱ABCD中,AB=6,AD=9,AF平分∠BAD交BC于点E,交DC的延长线于点F,BG⊥AF于点G,BG=4 ,EF= AE,则△CEF的周长为( ). A、8 B、10 C、14 D、163.
A、8 B、10 C、14 D、163.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )
 A、16 B、17 C、18 D、194.
A、16 B、17 C、18 D、194.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长( )
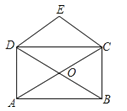 A、4 B、6 C、8 D、105. 如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为( )
A、4 B、6 C、8 D、105. 如图,在菱形ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=a,则菱形ABCD的周长为( ) A、16a B、12a C、8a D、4a6. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )
A、16a B、12a C、8a D、4a6. 如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( ) A、 B、2 C、 +1 D、2 +17. 菱形的周长为40,它的一条对角线长为12,则菱形的面积为( )A、24 B、48 C、96 D、1928.
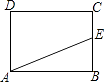
A、 B、2 C、 +1 D、2 +17. 菱形的周长为40,它的一条对角线长为12,则菱形的面积为( )A、24 B、48 C、96 D、1928.如图,矩形ABCD中,AB=4,BC=3,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数关系用图象表示正确的是( )
 A、
A、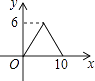 B、
B、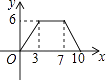 C、
C、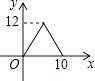 D、
D、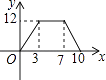 9. 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
9. 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( ) A、BP•BE=2 B、BP•BE=4 C、 = D、 =10. 如图,矩形ABCD的面积为1cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
A、BP•BE=2 B、BP•BE=4 C、 = D、 =10. 如图,矩形ABCD的面积为1cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,菱形ABCD的周长为36cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于 .
 12. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于度.
12. 如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于度.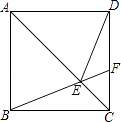 13. 在数学课上,老师提出如下问题:
13. 在数学课上,老师提出如下问题:如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.
小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是 .
 14. 如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为 .
14. 如图,矩形ABCD中,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=8,DC=6,则BE的长为 . 15. 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.
15. 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度. 16. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 .
16. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 . 17. 如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为 .
17. 如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为 . 18. 如图,直线l是矩形ABCD的一条对称轴,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有个.
18. 如图,直线l是矩形ABCD的一条对称轴,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有个.
三、计算题
-
19. 已知:如图,点E,F分别为▱ABCD的边BC,AD上的点,且∠1=∠2.
求证:AE=CF.
 20. 如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.
20. 如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF. (1)、求证:四边形AECF是平行四边形;(2)、若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.21. 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)、求证:四边形AECF是平行四边形;(2)、若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.21. 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE. (1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.22. 如图6所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.22. 如图6所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF. (1)、求证:D是BC的中点;(2)、若AB=AC,试判断四边形AFBD的形状,并证明你的结论.23. 在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
(1)、求证:D是BC的中点;(2)、若AB=AC,试判断四边形AFBD的形状,并证明你的结论.23. 在学习了正方形后,数学小组的同学对正方形进行了探究,发现: (1)、如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N.此时,有结论AE=MN,请进行证明;(2)、如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD,MN 与BD交于点G,连接BF,此时有结论:BF=FG,请利用图2做出证明.(3)、如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.24. 在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)、如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N.此时,有结论AE=MN,请进行证明;(2)、如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD,MN 与BD交于点G,连接BF,此时有结论:BF=FG,请利用图2做出证明.(3)、如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.24. 在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F. (1)、在图1中证明CE=CF;
(1)、在图1中证明CE=CF;
(2)、若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;(3)、若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.