2017-2018学年数学沪科版八年级下册第18章 勾股定理 单元检测
试卷更新日期：2018-06-01 类型：单元试卷
一、选择题
-
1. 下列说法中正确的是（ ）A、已知 是三角形的三边，则 B、在直角三角形中，两边的平方和等于第三边的平方 C、在Rt△
中，∠ 
°，所以
D、在Rt△ 中，∠ 
°，所以
2. 一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（ ）A、4 B、8 C、10 D、123. 已知△ABC的三边长分别是6cm、8cm、10cm，则△ABC的面积是（ ）A、24cm2 B、30cm2 C、40cm2 D、48cm24. 在△ABC中，若a=n2﹣1，b=2n，c=n2+1，则△ABC是（ ）A、锐角三角形 B、钝角三角形 C、等腰三角形 D、直角三角形5. 在Rt△ABC中，∠C=90°，AC=9，BC=12，则点C到AB的距离是（ ）A、 B、 C、 D、6. 以下各组数为三角形的三条边长，其中能作成直角三角形的是（ ）A、2，3，4 B、4，5，6 C、1， ， D、2， ，47. 若一直角三角形的两边长分别是6，8，则第三边长为（ ）A、10 B、2 C、10或2 D、148. 如图，在6个边长为1的小正方形及其部分对角线构成的图形中，如图从A点到B点只能沿图中的线段走，那么从A点到B点的最短距离的走法共有（ ）
A、1种 B、2种 C、3种 D、4种9. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8m处，发现此时绳子末端距离地面2m，则旗杆的高度为（滑轮上方的部分忽略不计）为（ ）
A、12m B、13m C、16m D、17m10. 如图，已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB= ．试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=（ ）
A、6 B、8 C、10 D、12二、填空题
-
11. 一个三角形三边满足（a+b）2﹣c2=2ab，则这个三角形是三角形．12. 如图，在△ABC中，AB=AC，∠BAC的角平分线交BC边于点D，AB=5，BC=6，则AD= ．
13. 在Rt△ABC中，∠C=90°，若a=40，b=9，则c=；若c=25，b=15，则a= ．14. 如图，有两棵树，一棵高12米，另一棵高6米，两树相距8米，一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行米．
15. 已知A，B，C三地位置如图所示，∠C=90°，A，C两地的距离是4km，B，C两地的距离是3km，则A，B两地的距离是km；若A地在C地的正东方向，则B地在C地的方向．
16. 如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为米（结果精确到0.1米，参考数据： =1.41， =1.73）．
17. 如图，一只蚂蚁从长、宽都是4，高是6的长方体纸箱的A点沿纸箱表面爬到B点，那么它所行的最短路线的长是 ．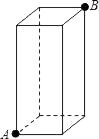
三、计算题
-
18. 如图，某会展中心在会展期间准备将高5m，长13m，宽2m的楼梯上铺地毯，已知地毯每平方米18元，请你帮助计算一下，铺完这个楼道至少需要多少元钱？
19. 如图，一高层住宅发生火灾，消防车立即赶到距大厦9米处（车尾到大厦墙面），升起云梯到火灾窗口，已知云梯长15米，云梯底部距地面2米，问：发生火灾的住户窗口距离地面多高？
20. 如图，在长方体 中， ，AD＝3，一只蚂蚁从A点出发，沿长方体表面爬到 点，求蚂蚁怎样走路程最短，最短路程是多少？
21. 如图，在B港有甲、乙两艘渔船，若甲船沿北偏东60°方向以每小时8海里速度前进，乙船沿南偏东某方向以每小时15海里速度全速前进，2小时后甲船到M岛，乙船到P岛，两岛相距34海里，你知道乙船沿那个方向航行吗？
22. 如图，△ABC是等腰直角三角形，延长BC至E使BE=BA，过点B作BD⊥AE于点D，BD与AC交于点F，连接EF．
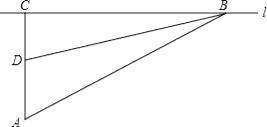
(1)、求证：BF=2AD；(2)、若CE= ，求AC的长．23. 校车安全是近几年社会关注的热点问题，安全隐患主要是超速和超载．某中学九年级数学活动小组进行了测试汽车速度的实验，如图，先在笔直的公路l旁选取一点A，在公路l上确定点B、C，使得AC⊥l，∠BAC=60°，再在AC上确定点D，使得∠BDC=75°，测得AD=40米，已知本路段对校车限速是50千米/时，若测得某校车从B到C匀速行驶用时10秒，问这辆车在本路段是否超速？请说明理由（参考数据： =1.41， =1.73）