2017-2018学年数学沪科版八年级下册19.2.2平行四边形的判定 同步练习

试卷更新日期：2018-06-01 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 已知：如图，四边形ABCD的两对角线AC，BD相交于点O，下列条件中，不能判定四边形ABCD是平行四边形的是（    ）

    A、AB=CD，AD=BC B、AB∥CD，AD=BC C、AB∥CD，AD∥BC D、OA=OC，OB=OD

    查看试题解析

  • 2. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（   ）

    A、①，② B、①，④ C、③，④ D、②，③

    查看试题解析

  • 3. 如图，在▱ABCD中，已知∠ODA=90°，AC=10cm，BD=6cm，则AD的长为（ ）

    A、4cm B、5cm C、6cm D、8cm

    查看试题解析

  • 4. 如图，▱ABCD的对角线交于点O，且AB=5，△OCD的周长为23，△OAD的周长是26 ，则平行四边形ABCD的周长是（    ）

    A、49 B、28 C、30 D、26

    查看试题解析

  • 5. 如图，▱ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（    ）

    A、18 B、28 C、36 D、46

    查看试题解析

  • 6. 四边形形ABCD中，AD‖BC，要判定四边形ABCD是平行四边形，还应满足（     ）
    A、∠A＋∠C＝180° B、∠B＋∠D＝180° C、∠A＋∠B＝180° D、∠A＋∠D＝180°

    查看试题解析

  • 7. 四边形ABCD的四个角∠A∶∠B∶∠C∶∠D满足下列哪一条件时，四边形ABCD是平行四边形（   ）

    A、1∶2∶2∶1 B、2∶1∶1∶1 C、1∶2∶3∶4 D、2∶1∶2∶1

    查看试题解析

  • 8. 如图，图1、图2、图3分别表示甲、乙、丙三人由甲A地到B地的路线图（箭头表示行进的方向）．其中E为AB的中点，AH＞HB，判断三人行进路线长度的大小关系为（    ）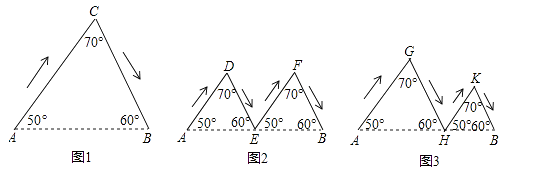

    A、甲＜乙＜丙 B、乙＜丙＜甲 C、丙＜乙＜甲 D、甲=乙=丙

    查看试题解析

二、填空题

  • 9. 一个四边形的边长依次为a，b，c，d，且a2+b2+c2+d2＝2ac+2bd，则这个四边形是。

    查看试题解析

  • 10. 如图，在四边形ABCD中，AB∥CD，AD∥BC，AC、BD相交于点O.若AC=6，则线段AO的长度等于.

    查看试题解析

  • 11. 如图，在△ABC中，AB=AC=5，D是BC上的点，DE∥AB交AC于点E，DF∥AC交AB于点F，那么四边形AFDE的周长是。

    查看试题解析

  • 12. 如图所示，已知E，F，G，H是四边形ABCD各边的中点，则S四边形EFGH：S四边形ABCD的值是 ．

    查看试题解析

  • 13. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是 ． （把所有正确结论的序号都填在横线上）

    ①∠DCF=∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．

    查看试题解析

三、计算题

  • 14. 已知：如图，在四边形ABCD中，DE⊥AC，BF⊥AC，垂足分别为E，F，DE=BF，∠ADB=∠CBD．求证：四边形ABCD是平行四边形．

    查看试题解析

  • 15. 如图，E，F是四边形ABCD的对角线AC上两点，AF＝CE，DF＝BE，DF∥BE．

    求证：

    (1)、△AFD≌△CEB；
    (2)、四边形ABCD是平行四边形．

    查看试题解析

  • 16. 如图，在△ABC中，∠ACB=90°，CD⊥AB垂足为D，AE平分∠CAB交CD于点F，交BC于点E，EH⊥AB，垂足为H，连接FH．

    求证：

    (1)、CF=CE
    (2)、四边形CFHE是平行四边形．

    查看试题解析

  • 17. 如图，平行四边形ABCD中，∠ABC=60°，点E，F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，CF= 3 ．

    (1)、求证：四边形ABDE是平行四边形；
    (2)、求AB的长．

    查看试题解析