2017-2018学年数学沪科版八年级下册19.2.1平行四边形的性质 同步练习
试卷更新日期：2018-06-01 类型：同步测试
一、选择题
-
1. 如图，在▱ABCD中，∠D=120°，则∠A的度数等于（ ）
A、120° B、60° C、40° D、30°2. 如图，▱ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为（ ）
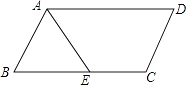A、1 B、2 C、3 D、43. 平行四边形ABCD 中，有两个内角的比为1：2，则这个平行四边形中较小的内角是（ ）A、45° B、60° C、90° D、120°4. 如图，平行四边形ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE等于（ ）
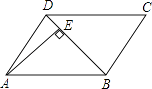A、20° B、25° C、30° D、35°5. 如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO的周长是（ ）
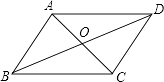A、10 B、14 C、20 D、226. 如图，在▱ABCD中，延长AB到点E，使BE=AB，连接DE交BC于点F，则下列结论不一定成立的是（ ）
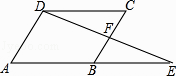A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF7. 如图，在▱ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B＝52°，∠DAE＝20°，则∠FED′的大小为_______．
A、36° B、52° C、48° D、30°8. 如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（ ）①∠DCF= ∠BCD；②EF=CF；③∠DFE=3∠AEF；④S△BEC=2S△CEF ．
A、①②③ B、②③④ C、①②④ D、①③④二、填空题
-
9. 如图，在平行四边形ABCD中，BE平分∠ABC，交AD于点E，AB=3cm，ED= cm，则平行四边形ABCD的周长是 ．
10. 阅读下面材料：在数学课上，老师提出如下问题：
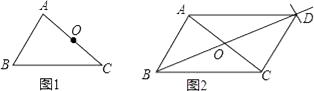
已知：如图1，△ABC及AC边的中点O．
求作：平行四边形ABCD．
小敏的作法如下：
①连接BO并延长，在延长线上截取OD=BO；
②连接DA、DC．所以四边形ABCD就是所求作的平行四边形．
老师说：“小敏的作法正确．”
请回答：小敏的作法正确的理由是 ．
11. 在▱ABCD中，BC边上的高为4，AB=5，AC=2 ，则▱ABCD的周长等于 ．12. 如图所示，在▱ABCD中，∠C=40°，过点D作AD的垂线，交AB于点E，交CB的延长线于点F，则∠BEF的度数为 ．
13. 如图，□ ABCD中，E是BA延长线上一点，AB＝AE，连结CE交AD于点F，若CF平分∠BCD，AB＝3，则BC的长为 ．
14. 如图，▱ABCD中，AB=2，BC=4，∠B=60°，点P是四边形上的一个动点，则当△PBC为直角三角形时，BP的长为 ．
三、计算题
-
15. 如图，平行四边形ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点，若AC+BD=24，△OAB的周长是18，试求EF的长．
